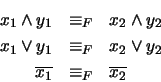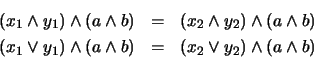


Posterior: Ultraproductos
Arriba: Filtros y homomorfismos
Anterior: Filtros y ultrafiltros
Definición 4.4
Sean
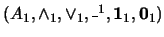
y
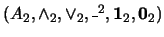
dos álgebras booleanas. Una función
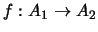
es un
HOMOMORFISMO DE ÁLGEBRAS BOOLEANAS si satisface las siguientes relaciones:
-
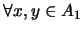 :
:
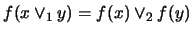 .
.
-
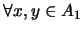 :
:
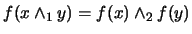 .
.
-
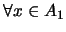 :
:
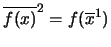 .
.
El conjunto
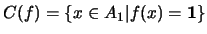
se dice ser la
CORAZA de
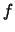
en tanto que el conjunto
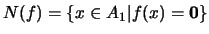
es el
NÚCLEO de
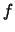
.
Observación 4.5
Si
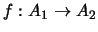
es un homomorfismo entonces su coraza
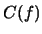
es un filtro y su núcleo
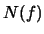
es un ideal.
Definición 4.5
Sea
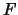
un filtro en un álgebra booleana

. Definamos la relación en

siguiente:
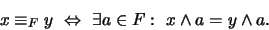 |
(2) |
Se observa inmediatamente que 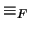 es una relación de equivalencia que es además congruente con las operaciones del álgebra booleana: Si
es una relación de equivalencia que es además congruente con las operaciones del álgebra booleana: Si
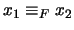 e
e
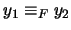 entonces
entonces
En efecto, si
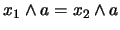 y
y
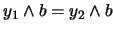 , con
, con 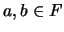 entonces, evidentemente:
entonces, evidentemente:
y también
Así pues, el cociente 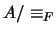 es también un álgebra booleana con las operaciones
es también un álgebra booleana con las operaciones
![\begin{displaymath}
\begin{array}{lcl}
\land_c: \left(\left[x\right],\left[y\r...
...ft[x\right]}^c = \left[\overline{x}\right] %%\\
\end{array}
\end{displaymath}](img333.png) |
(3) |
La función proyección
![$\pi_F:x\mapsto \left[x\right]$](img334.png) es un homomorfismo. Un elemento
es un homomorfismo. Un elemento 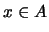 está en la coraza de
está en la coraza de 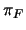 si
si
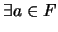 :
:
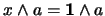 . Pero, siendo
. Pero, siendo 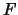 un filtro, esto último es equivalente a que
un filtro, esto último es equivalente a que 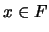 . En otras palabras, la coraza de la proyección es el filtro
. En otras palabras, la coraza de la proyección es el filtro 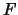 . Un elemento
. Un elemento 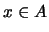 está en el núcleo de
está en el núcleo de 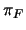 si
si
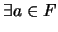 :
:
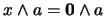 . Pero, siendo
. Pero, siendo 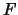 un filtro, esto último es equivalente a que
un filtro, esto último es equivalente a que
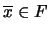 . El núcleo es pues el conjunto de elementos cuyos complementos están en el filtro
. El núcleo es pues el conjunto de elementos cuyos complementos están en el filtro 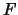 .
.
Definición 4.6
Un filtro
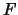
en un álgebra booleana se dice ser
PRIMO si para cualesquiera dos elementos
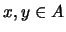
rige la implicación siguiente:
La proposición siguiente proporciona diversos criterios para decidir cuándo un filtro es un ultrafiltro.
Demostración
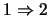 ) Sea
) Sea 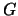 un filtro que contenga
un filtro que contenga 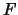 . Entonces
. Entonces 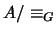 es un subálgebra de
es un subálgebra de 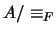 , pues para cada
, pues para cada 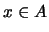 :
:
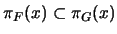 . Pero como
. Pero como 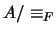 es la mínima álgebra booleana,
es la mínima álgebra booleana, 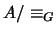 ha de coincidir con ella. Por tanto
ha de coincidir con ella. Por tanto 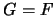 .
.
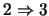 ) Sean
) Sean 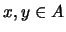 tales que
tales que 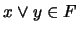 . Supongamos que
. Supongamos que 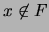 . Entonces, al ser
. Entonces, al ser 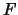 un ultrafiltro, el filtro generado por
un ultrafiltro, el filtro generado por 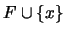 ha de ser todo
ha de ser todo  . Así, existe
. Así, existe 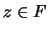 tal que
tal que
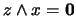 . Ahora, por un lado,
. Ahora, por un lado,
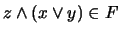 como inter de dos elementos en
como inter de dos elementos en 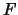 , pero por otro lado:
, pero por otro lado:
Vale decir, 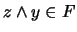 . Por tanto,
. Por tanto, 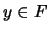 .
.
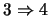 ) Para cualquier
) Para cualquier 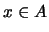 , se tiene
, se tiene
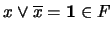 . Al ser
. Al ser 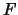 primo resulta la relación 4.
primo resulta la relación 4.
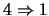 ) Tenemos que para cada
) Tenemos que para cada 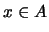 ,
, 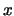 está en la coraza o en el núcleo de
está en la coraza o en el núcleo de 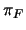 . Por tanto el álgebra cociente consta sólo de dos elementos.
. Por tanto el álgebra cociente consta sólo de dos elementos.  Sea
Sea
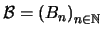 una sucesión (numerable) de conjuntos en un álgebra booleana
una sucesión (numerable) de conjuntos en un álgebra booleana  tal que
tal que
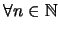 :
:
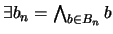 . Se dice que un ultrafiltro
. Se dice que un ultrafiltro 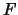 PRESERVA LAS INTERSECCIONES de
PRESERVA LAS INTERSECCIONES de 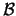 si se cumple:
si se cumple:
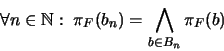 |
(4) |
Teorema 4.2 (Lema de Tarski)
Sea
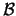
como antes. Si
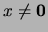
es un elemento no nulo en el álgebra booleana

, entonces existe un ultrafiltro
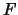
que contiene a
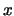
y preserva las intersecciones en
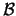
.
Demostración
Construiremos una sucesión
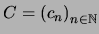 tal que para cada
tal que para cada
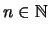 :
:
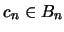 , y
, y
-
![$\{x\}\cup\{b_m\lor \overline{c_m}\vert m\in[\![0,n]\!]\}$](img366.png) tiene la propiedad de intersección finita.
tiene la propiedad de intersección finita.
Inicialmente, para 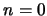 , observemos que existe un
, observemos que existe un 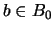 tal que
tal que
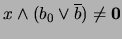 . En efecto, si se supusiese lo contrario entonces para cada
. En efecto, si se supusiese lo contrario entonces para cada 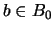 :
:
y por tanto
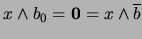 . La segunda igualdad implica
. La segunda igualdad implica 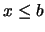 , para todo
, para todo 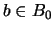 . En consecuencia,
. En consecuencia, 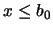 , pues
, pues 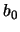 es el ínfimo de los elementos en
es el ínfimo de los elementos en 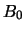 . Así pues:
. Así pues:
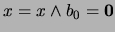 lo cual contradice la hipótesis convenida para
lo cual contradice la hipótesis convenida para 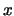 . Elijamos pues
. Elijamos pues 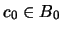 tal que
tal que
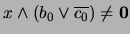 .
Ahora, sea
.
Ahora, sea 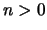 y supongamos que se ha elegido
y supongamos que se ha elegido
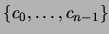 con las propiedades requeridas. Hagamos
con las propiedades requeridas. Hagamos
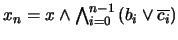 . Por la propiedad de intersección finita,
. Por la propiedad de intersección finita,
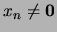 . Igual que antes, observemos que existe un
. Igual que antes, observemos que existe un 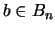 tal que
tal que
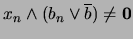 . En efecto, si se supusiese lo contrario entonces para cada
. En efecto, si se supusiese lo contrario entonces para cada 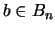 :
:
y por tanto
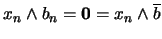 . La segunda igualdad implica
. La segunda igualdad implica 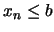 , para todo
, para todo 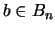 . En consecuencia,
. En consecuencia, 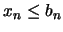 , pues
, pues 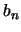 es el ínfimo de los elementos en
es el ínfimo de los elementos en 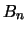 . Así pues:
. Así pues:
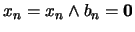 lo cual contradice la propiedad exigida para
lo cual contradice la propiedad exigida para 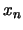 . Elijamos pues
. Elijamos pues 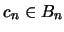 tal que
tal que
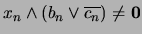 .
De esta manera, el conjunto
.
De esta manera, el conjunto
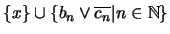 tiene la propiedad de intersección finita. Sea
tiene la propiedad de intersección finita. Sea 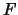 un ultrafiltro que lo contenga.
un ultrafiltro que lo contenga. 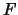 contiene pues a
contiene pues a 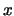 . Veamos que preserva las intersecciones de
. Veamos que preserva las intersecciones de 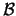 .
Como cada elemento de la forma
.
Como cada elemento de la forma
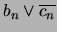 está en
está en 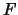 se tiene
se tiene
y en consecuencia
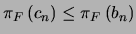 . Como
. Como 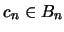 , esta última desigualdad entraña:
, esta última desigualdad entraña:
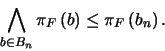 |
(5) |
Pero, por otro lado, 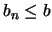 para cada
para cada 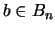 . Al ser
. Al ser 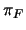 un homomorfismo,
un homomorfismo,
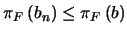 y por tanto
y por tanto
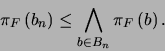 |
(6) |
De las ecuaciones (5) y (6) obtenemos que 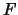 , en efecto, preserva las intersecciones de
, en efecto, preserva las intersecciones de 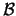 .
. 



Posterior: Ultraproductos
Arriba: Filtros y homomorfismos
Anterior: Filtros y ultrafiltros
Guillermo Morales-Luna
2004-07-27
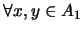 :
:
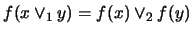 .
.
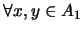 :
:
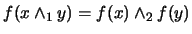 .
.
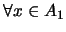 :
:
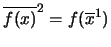 .
.