

Posterior: Programas
Arriba: Estructuras algebraicas básicas
Anterior: Lecturas recomendadas
1. Sean 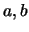 y
y 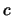 tres elementos en un retículo
tres elementos en un retículo 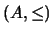 . Muestre que vale la siguiente implicación:
. Muestre que vale la siguiente implicación:
2. Sean 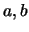 dos elementos en un retículo
dos elementos en un retículo 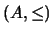 . Muestre que vale la siguiente equivalencia:
. Muestre que vale la siguiente equivalencia:
3. Sea
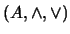 un sistema algebraico donde las operaciones binarias
un sistema algebraico donde las operaciones binarias
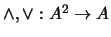 satisfacen las leyes de absorción. Muestre que necesariamente han de ser idempotentes.
satisfacen las leyes de absorción. Muestre que necesariamente han de ser idempotentes.
4. Dibuje el retículo formado por los divisores de 240.
5. Sea 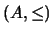 un conjunto ordenado finito. Muestre que las siguientes dos proposiciones son equivalentes a pares:
un conjunto ordenado finito. Muestre que las siguientes dos proposiciones son equivalentes a pares:
-
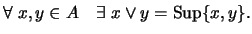
 posee un elemento máximo.
posee un elemento máximo.
En la prueba de la equivalencia anterior, ¿es posible omitir la hipótesis de que  es finito?
es finito?
6. Un retículo 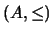 se dice ser modular si
se dice ser modular si
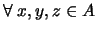 rige la implicación siguiente:
rige la implicación siguiente:
Encuentre un retículo con cinco elementos que no sea modular.
7. Muestre que para cualesquiera cuatro elementos 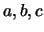 y
y 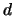 en un retículo
en un retículo  cualquiera ha de cumplirse la desigualdad siguiente:
cualquiera ha de cumplirse la desigualdad siguiente:
8. Dibuje cinco retículos (esencialmente) distintos con menos de cinco elementos estrictamente. ¿Puede encontrar alguno más?
9. Sea  un retículo con más de 6 elementos. Muestre que existe un subconjunto
un retículo con más de 6 elementos. Muestre que existe un subconjunto
de 6 elementos de  que forma un subretículo de
que forma un subretículo de  , es decir, tal que
, es decir, tal que
10. Sea  un retículo con
un retículo con 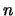 elementos:
elementos:
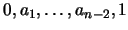 ; en el que
; en el que
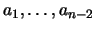 son
son 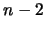 sucesores de
sucesores de 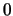 y, naturalmente, antecesores también de
y, naturalmente, antecesores también de 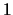 . Muestre que
. Muestre que  es modular.
es modular.
11. Sean
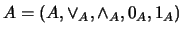 y
y
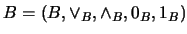 dos retículos. El retículo producto es
dos retículos. El retículo producto es
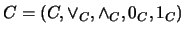 , donde
, donde
y
Muestre que 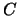 es un retículo. ¿Cuáles son sus elementos máximo y mínimo?
es un retículo. ¿Cuáles son sus elementos máximo y mínimo?
12. Muestre que el producto de dos retículos modulares es modular.
13. Muestre que en un álgebra booleana se cumple que 
14. Sea  un álgebra booleana. Demuestre la
Ley de Porecki:
un álgebra booleana. Demuestre la
Ley de Porecki:
15. Sea  un álgebra booleana. Dados
un álgebra booleana. Dados 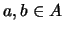 el intervalo
el intervalo ![$[a,b]$](img460.png) es la intersección del cono superior de
es la intersección del cono superior de 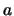 con el cono inferior de
con el cono inferior de 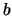 , en otras palabras
, en otras palabras
- Muestre que
![$I_{a,b}=[a,b]$](img463.png) es un álgebra booleana.
es un álgebra booleana.
- Determine a los elementos
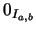 y
y 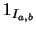 .
.
- Dado
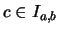 , ¿cuál es el elemento
, ¿cuál es el elemento 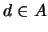 que es complemento de
que es complemento de 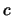 en
en 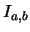 ?
?
16. Muestre que el producto de dos álgebras booleanas es un álgebra booleana. ¿Cuál es la longitud del álgebra producto?
17. Demuestre o refute cada una de las siguientes igualdades propuestas en un álgebra booleana:
-
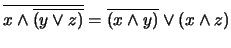 .
.
-
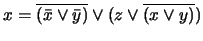 .
.
18. Muestre que el conjunto de divisores de 1155 forma un álgebra booleana. ¿Cuál es su longitud?.
19. Decida si acaso los divisores de 4620 forman un álgebra booleana.
20. Dé condiciones necesarias y suficientes para que un número 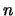 sea tal que sus divisores formen un álgebra booleana.
sea tal que sus divisores formen un álgebra booleana.
21. Muestre que toda álgebra booleana es un retículo modular (vea la definición más arriba).
22. Muestre que si un conjunto 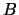 en un álgebra booleana
en un álgebra booleana  tiene la propiedad de intersección finita entonces para cualquier elemento
tiene la propiedad de intersección finita entonces para cualquier elemento 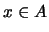 uno de los dos conjuntos
uno de los dos conjuntos 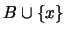 o
o
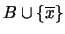 también la tiene.
también la tiene.
23. Sea
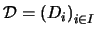 una cadena en un álgebra booleana
una cadena en un álgebra booleana  (para cualesquiera dos elementos en
(para cualesquiera dos elementos en 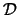 , uno está contenido en el otro). Muestre que si cada
, uno está contenido en el otro). Muestre que si cada 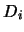 tiene la propiedad de intersección finita entonces también la tiene la unión
tiene la propiedad de intersección finita entonces también la tiene la unión
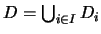 .
.
24. Sea 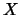 un conjunto no vacío. Muestre que un ultrafiltro
un conjunto no vacío. Muestre que un ultrafiltro 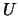 en el álgebra booleana de sus partes,
en el álgebra booleana de sus partes,
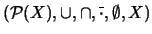 es principal si y sólo si hay un conjunto finito en
es principal si y sólo si hay un conjunto finito en 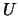 .
Muestre entonces que si
.
Muestre entonces que si 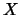 es finito, entonces todos los ultrafiltros en
es finito, entonces todos los ultrafiltros en 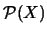 han de ser principales.
han de ser principales.
25. Construya un conjunto 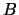 en un álgebra booleana
en un álgebra booleana  tal que
tal que
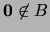 , el inter de cualesquiera dos elementos en
, el inter de cualesquiera dos elementos en 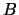 no es
no es 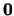 , pero
, pero 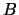 no tiene la propiedad de intersección finita.
no tiene la propiedad de intersección finita.



Posterior: Programas
Arriba: Estructuras algebraicas básicas
Anterior: Lecturas recomendadas
Guillermo Morales-Luna
2004-07-27