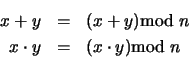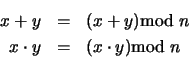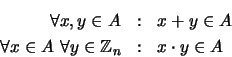


Posterior: Cálculo proposicional
Arriba: Estructuras algebraicas básicas
Anterior: Ejercicios
1. Escriba un ensayo sobre la artimética de punto flotante. Indique
criterios para decidir cuándo un número real está o no dentro de esa
aritmética. Consulte el ANSI/IEEE 754-1985 IEEE Standard for Binary Floating-Point Arithmetic, The Institute of Electrical and Electronics Engineers, Inc., New York, 1985, http://www.wikipedia.com/wiki/IEEE_Floating_Point_Standard
2. Escriba un programa que dados
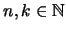 ,
, 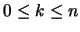 , encuentre todos los subconjuntos de
, encuentre todos los subconjuntos de 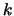 elementos en el conjunto de índices entre 0, y
elementos en el conjunto de índices entre 0, y 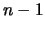 ,
, ![$[\![0,n-1]\!]$](img479.png) .
.
3. Escriba un programa que dado
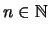 , encuentre todos los subconjuntos del conjunto
, encuentre todos los subconjuntos del conjunto ![$[\![0,n-1]\!]$](img479.png) .
.
4. Sea 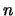 un entero mayor que 1 y sea
un entero mayor que 1 y sea
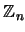 el conjunto de residuos módulo
el conjunto de residuos módulo 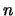 .
.
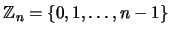 . Considere las operaciones suma y producto que coinciden con las usuales de los enteros
. Considere las operaciones suma y producto que coinciden con las usuales de los enteros 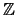 pero tomando residuos módulo
pero tomando residuos módulo 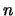 :
:
Escriba un programa que dado 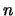 escriba las tablas de operaciones
escriba las tablas de operaciones 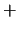 y
y 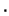 de
de
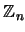 .
Observación: El reloj de carátula en su cocina seguramente le puede dar una idea de la suma en
.
Observación: El reloj de carátula en su cocina seguramente le puede dar una idea de la suma en
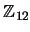 (ahí 12=0 pues la medianoche es lo mismo que las cero horas, ¿verdad?).
(ahí 12=0 pues la medianoche es lo mismo que las cero horas, ¿verdad?).
5. Sea 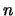 un entero mayor que 1. Un ideal en
un entero mayor que 1. Un ideal en
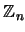 es un subconjunto
es un subconjunto
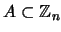 que es cerrado bajo la suma y que ``absorbe productos'':
que es cerrado bajo la suma y que ``absorbe productos'':
Por ejemplo, el conjunto 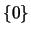 siempre es un ideal, y el conjunto
siempre es un ideal, y el conjunto 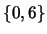 es un ideal en
es un ideal en
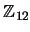 .
Escriba un programa que dado
.
Escriba un programa que dado 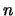 encuentre todos los ideales de
encuentre todos los ideales de
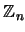 .
.
6. Si
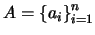 es un conjunto de
es un conjunto de 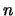 elementos y
elementos y 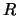 es una
relación en
es una
relación en  ,
,
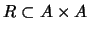 , la matriz de incidencia de
, la matriz de incidencia de 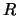 es
es
![$M_R=\left[m_{ij}\right]_{i=1,\ldots,n}^{j=1,\ldots,n}\in\{0,1\}^{n\times n}$](img493.png) tal que
tal que
Dadas dos relaciones
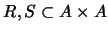 , la composición
, la composición
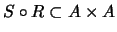 se define como sigue:
se define como sigue:
Por ejemplo, piense que  es el conjunto de alumnos,
es el conjunto de alumnos, 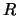 es la relación ``está en el mismo grado que'' y
es la relación ``está en el mismo grado que'' y 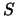 es la relación ``es amigo de''. Entonces se tendrá que
es la relación ``es amigo de''. Entonces se tendrá que 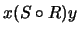 si es que un amigo de
si es que un amigo de 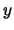 está en el mismo grado que
está en el mismo grado que 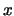 .
Escriba un programa que reciba las matrices de incidencia de
.
Escriba un programa que reciba las matrices de incidencia de 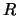 y de
y de 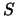 y calcule la matriz de incidencia de
y calcule la matriz de incidencia de 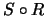 .
.
7. Escriba un programa que lea la matriz de incidencia de una relación y decida si la relación que representa es de orden.
8. Escriba un programa que lea un número entero 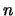 y genere de manera aleatoria una relación de orden en el conjunto
y genere de manera aleatoria una relación de orden en el conjunto ![$[\![0,n-1]\!]$](img479.png) . La salida de este programa ha de ser la matriz de incidencia de la relación generada.
. La salida de este programa ha de ser la matriz de incidencia de la relación generada.
9. Escriba un programa que lea las matrices de incidencia de dos relaciones de orden 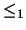 y
y 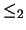 , y construya la matriz de incidencia de la relación producto. Recordamos que si
, y construya la matriz de incidencia de la relación producto. Recordamos que si 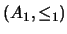 y
y 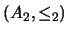 son dos relaciones de orden entonces el orden producto
son dos relaciones de orden entonces el orden producto 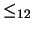 está definido en el producto cartesiano
está definido en el producto cartesiano 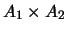 mediante la relación:
mediante la relación:
10. Sea 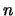 un entero positivo. A todo subconjunto
un entero positivo. A todo subconjunto 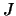 del conjunto
del conjunto ![$[\![0,n-1]\!]$](img479.png) lo identificamos por la lista de valores de su función característica:
lo identificamos por la lista de valores de su función característica:
![$\mbox{\boldmath$\epsilon$}_J=\left[\epsilon_j\right]_{j=0}^{n-1}$](img506.png) , donde
, donde 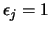 si
si 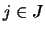 y
y 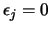 si
si 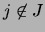 . Ahora bien, a cada vector
. Ahora bien, a cada vector
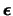 de 0's y 1's lo podemos leer como la representación en base 2 de un entero
de 0's y 1's lo podemos leer como la representación en base 2 de un entero
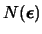 en el intervalo
en el intervalo
![$[\![0,2^n-1]\!]$](img513.png) , donde el bit más significativo está más a la derecha (es decir, la representación en base 2 de
, donde el bit más significativo está más a la derecha (es decir, la representación en base 2 de
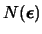 es el reverso de la palabra
es el reverso de la palabra
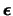 ). Por ejemplo, para
). Por ejemplo, para 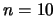 , si
, si
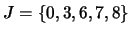 entonces:
entonces:
La correspondencia
![$\phi:{\cal P}([\![0,n-1]\!])\to [\![0,2^n-1]\!]$](img517.png) ,
,
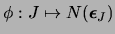 , es una biyección. Sea
, es una biyección. Sea
![$\psi:[\![0,2^n-1]\!]\to {\cal P}([\![0,n-1]\!])$](img519.png) su función inversa.
Pues bien, definamos en
su función inversa.
Pues bien, definamos en
![$[\![0,2^n-1]\!]$](img513.png) el orden siguiente:
el orden siguiente:
Escriba un programa que dado 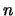 escriba la matriz de incidencia del orden
escriba la matriz de incidencia del orden 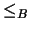 en
en
![$[\![0,2^n-1]\!]$](img513.png) .
Sugerencia: Podría utilizar, para simplificar todo, funciones primitivas de C del tipo de datos unsigned integer, por ejemplo.
.
Sugerencia: Podría utilizar, para simplificar todo, funciones primitivas de C del tipo de datos unsigned integer, por ejemplo.
11. Escriba un programa que dada la matriz de incidencia de una relación de orden, digamos
![$M=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img521.png) , escriba, para cada elemento
, escriba, para cada elemento
![$j\in [\![0,n-1]\!]$](img522.png) la lista de sus sucesores y la lista de sus antecesores y que señale cuáles elementos son el mínimo y el máximo, si los hubiera. Recordamos que los sucesores de un elemento son los elementos minimales de su cono superior en tanto que los antecesores de un elemento son los elementos maximales de su cono inferior, privados ambos conos del elemento que los define.
la lista de sus sucesores y la lista de sus antecesores y que señale cuáles elementos son el mínimo y el máximo, si los hubiera. Recordamos que los sucesores de un elemento son los elementos minimales de su cono superior en tanto que los antecesores de un elemento son los elementos maximales de su cono inferior, privados ambos conos del elemento que los define.
12. Sea
![$A=\left\{a_{i}\right\}_{i\in [\![0,n-1]\!]}$](img523.png) un conjunto con
un conjunto con 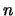 elementos y sea
elementos y sea
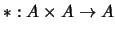 una operación de aridad 2. La tabla de operación de
una operación de aridad 2. La tabla de operación de  es la matriz
es la matriz
![$M_*=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img525.png) con entradas en el conjunto
con entradas en el conjunto ![$[\![0,n-1]\!]$](img479.png) tales que
tales que
Escriba un programa que dada la matriz de incidencia de una relación de orden, digamos
![$M=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img521.png) , escriba las tablas de las operaciones
, escriba las tablas de las operaciones
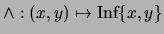 ,
,
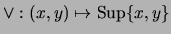 . Si para alguna pareja de elementos una de estas operaciones no estuviera definida, se ha de indicar este hecho poniendo un símbolo especial en la correspondiente entrada de esa operación.
. Si para alguna pareja de elementos una de estas operaciones no estuviera definida, se ha de indicar este hecho poniendo un símbolo especial en la correspondiente entrada de esa operación.
13. Escriba un programa que dadas las dos tablas de operaciones
![$M_{\land}=\left[m_{1ij}\right]_{i,j\in [\![0,n-1]\!]}$](img529.png) ,
,
![$M_{\lor}=\left[m_{2ij}\right]_{i,j\in [\![0,n-1]\!]}$](img530.png) de un retículo, calcule la matriz de incidencia del orden inducido por el retículo.
de un retículo, calcule la matriz de incidencia del orden inducido por el retículo.
14. Escriba un programa que lea la tabla
![$M_*=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img525.png) , con entradas en el conjunto
, con entradas en el conjunto ![$[\![0,n-1]\!]$](img479.png) , de alguna operación
, de alguna operación
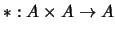 y que decida cuáles de las siguientes propiedades posee
y que decida cuáles de las siguientes propiedades posee 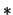 : Conmutatividad, asociatividad, idempotencia, existencia de unidades, existencia de inversos (en caso de que existan unidades).
: Conmutatividad, asociatividad, idempotencia, existencia de unidades, existencia de inversos (en caso de que existan unidades).
15. Escriba un programa que dada la matriz de incidencia de una relación de orden, digamos
![$M=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img521.png) , encuentre una cadena que se inicie en un elemento minimal y termine en un elemento maximal.
, encuentre una cadena que se inicie en un elemento minimal y termine en un elemento maximal.
16. Escriba un programa que lea un número entero 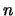 y escriba la tabla
y escriba la tabla
![$M_*=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img525.png) , con entradas en el conjunto
, con entradas en el conjunto ![$[\![0,n-1]\!]$](img479.png) , de alguna operación
, de alguna operación
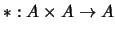 generada aleatoriamente.
Corra este programa
generada aleatoriamente.
Corra este programa 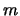 veces y cuente el número
veces y cuente el número 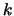 de tablas de operaciones asociativas. Muestre el cociente
de tablas de operaciones asociativas. Muestre el cociente 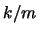 como una proporción de las operaciones asociativas.
como una proporción de las operaciones asociativas.
17. Escriba un programa que lea un número entero 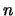 y escriba la tabla
y escriba la tabla
![$M_*=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img525.png) , con entradas en el conjunto
, con entradas en el conjunto ![$[\![0,n-1]\!]$](img479.png) , de alguna operación
, de alguna operación
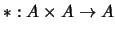 generada aleatoriamente que sea a la vez asociativa e idempotente.
Corra este programa
generada aleatoriamente que sea a la vez asociativa e idempotente.
Corra este programa 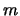 veces y cuente el número
veces y cuente el número 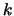 de tablas de operaciones asociativas e idempotentes. Muestre el cociente
de tablas de operaciones asociativas e idempotentes. Muestre el cociente 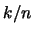 como una proporción de las operaciones asociativas e idempotentes.
como una proporción de las operaciones asociativas e idempotentes.
18. Escriba un programa que reciba dos enteros positivos no-nulos 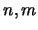 , calcule el mínimo común múltiplo
, calcule el mínimo común múltiplo 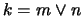 , enumere a los elementos en el cono inferior
, enumere a los elementos en el cono inferior 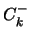 de
de 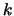 , en el orden de divisibilidad, y escriba las tablas de las operaciones
, en el orden de divisibilidad, y escriba las tablas de las operaciones 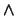 y
y 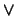 en
en 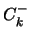 .
.
19. Escriba un programa que lea una tabla de operación
![$M=\left[m_{ij}\right]_{i,j\in [\![0,n-1]\!]}$](img521.png) y una permutación
y una permutación 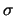 del conjunto de índices
del conjunto de índices ![$[\![0,n-1]\!]$](img479.png) y escriba la tabla
y escriba la tabla
![$\sigma(M)=\left[m_{\sigma(i),\sigma(j)}\right]_{i,j\in [\![0,n-1]\!]}$](img539.png) .
.
20. Escriba un programa que dadas dos tablas de operaciones
![$M_1=\left[m_{1ij}\right]_{i,j\in [\![0,n-1]\!]}$](img540.png) ,
,
![$M_2=\left[m_{2ij}\right]_{i,j\in [\![0,n-1]\!]}$](img541.png) decida si existe un retículo
decida si existe un retículo
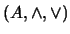 tal que
tal que 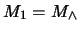 ,
, 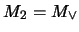 . En caso de que no exista tal retículo, explicar cuál es la causa.
. En caso de que no exista tal retículo, explicar cuál es la causa.
21. Escriba un programa que mediante un procedimiento de backtracking localice todas las cadenas de una relación de orden.
22. Sea
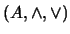 un retículo. Para un elemento
un retículo. Para un elemento 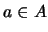 la altura
la altura 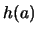 de
de 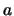 es el número de aristas en el camino más corto que conecta a
es el número de aristas en el camino más corto que conecta a 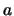 con el elemento mínimo del retículo. La altura del mínimo es 0, la de los sucesores del mínimo es 1, la de los sucesores de los sucesores del mínimo es 2, etc.
Escriba un programa que dadas las dos tablas de operaciones
con el elemento mínimo del retículo. La altura del mínimo es 0, la de los sucesores del mínimo es 1, la de los sucesores de los sucesores del mínimo es 2, etc.
Escriba un programa que dadas las dos tablas de operaciones
![$M_{\land}=\left[m_{1ij}\right]_{i,j\in [\![0,n-1]\!]}$](img529.png) ,
,
![$M_{\lor}=\left[m_{2ij}\right]_{i,j\in [\![0,n-1]\!]}$](img530.png) de un retículo, calcule para cada elemento
de un retículo, calcule para cada elemento 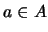 su altura
su altura 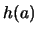 .
.



Posterior: Cálculo proposicional
Arriba: Estructuras algebraicas básicas
Anterior: Ejercicios
Guillermo Morales-Luna
2004-07-27