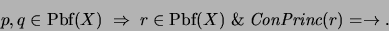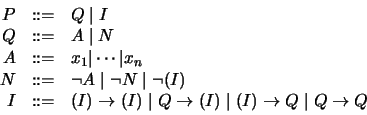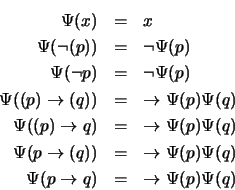- Si
 es una variable proposicional entonces
es una variable proposicional entonces  es una
proposición bien formada y su conectivo principal es vacío:
es una
proposición bien formada y su conectivo principal es vacío:
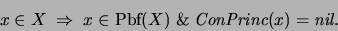
- Si
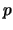 es una proposición, sea
es una proposición, sea 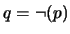 si el conectivo principal de
si el conectivo principal de 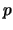 es
es  y sea
y sea 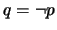 en otro caso.
en otro caso. 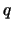 es la negación de
es la negación de 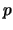 y es también una proposición:
y es también una proposición:
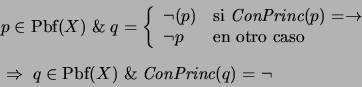
- Si
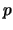 y
y 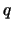 son dos proposiciones, definamos
son dos proposiciones, definamos
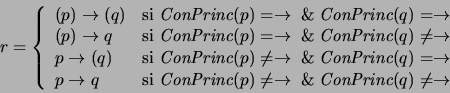
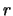 es la implicación de
es la implicación de 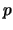 a
a 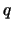 y es también una proposición:
y es también una proposición: