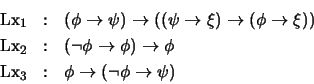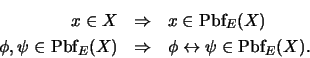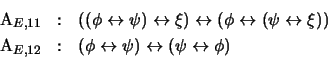


Posterior: Coherencia y completitud
Arriba: Cálculo proposicional
Anterior: Deducción natural
1. Encuentre las negaciones de las siguientes proposiciones:
-
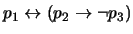
-
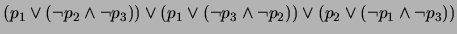
2. Sea
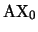 el conjunto de axiomas
el conjunto de axiomas
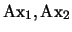 y
y
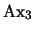 vistos en clase. Si para una proposición
vistos en clase. Si para una proposición  se tiene
se tiene 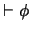 , escribiremos aquí
, escribiremos aquí
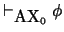 .
Sea
.
Sea
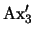 el siguiente esquema de axiomas:
el siguiente esquema de axiomas:
Sea
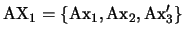 .
.
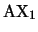 consiste de sustituir el esquema
consiste de sustituir el esquema
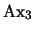 por
por
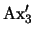 en
en
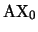 . La propiedad de ser demostrable en
. La propiedad de ser demostrable en
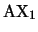 se define de igual manera que en
se define de igual manera que en
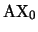 . Si
. Si  es un teorema en
es un teorema en
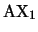 escribiremos
escribiremos
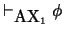 .
Demuestre la proposiciones siguientes:
.
Demuestre la proposiciones siguientes:
- El Teorema de Deducción es válido también para
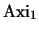 .
.
- Los axiomas de
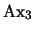 se pueden demostrar en
se pueden demostrar en
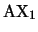 .
.
- Los axiomas de
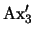 se pueden demostrar en
se pueden demostrar en
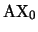 .
.
-
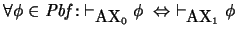 .
.
3. Escriba pruebas en
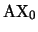 de los siguientes teoremas
de los siguientes teoremas
-
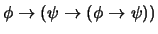 .
.
-
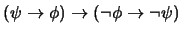
4. Sea
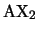 el sistema que se obtiene de
el sistema que se obtiene de
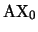 al añadir el esquema de axiomas
al añadir el esquema de axiomas
Muestre que
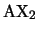 es formalmente inconsistente.
es formalmente inconsistente.
5. Ley de permutación de premisas. Muestre que cualesquiera que sean
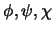 se tiene
se tiene
6. Exprese a la proposición
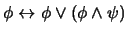 en términos de
en términos de 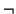 y
y 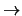 únicamente.
únicamente.
7. Muestre que la expresión resultante en el ejercicio anterior es un teorema.
8. Sea
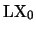 el conjunto de axiomas
el conjunto de axiomas
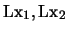 y
y
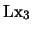 siguientes:
siguientes:
e introduzcamos la regla de modus ponens. Si para una proposición  se tiene
se tiene 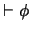 , escribiremos aquí
, escribiremos aquí
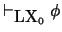 .
Decida si el sistema deductivo
.
Decida si el sistema deductivo
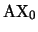 visto en clase subsume al
visto en clase subsume al
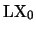 . Es decir, si para cualquier
. Es decir, si para cualquier  se cumple:
se cumple:
9. Decida si el sistema deductivo
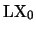 del ejercicio anterior subsume al
del ejercicio anterior subsume al
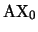 visto en clase. Es decir, si para cualquier
visto en clase. Es decir, si para cualquier  se cumple:
se cumple:
10. Subcálculo proposicional con la equivalencia. Considérese únicamente proposiciones con el conectivo
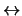 . Específicamente, si
. Específicamente, si
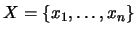 es un conjunto finito de variables
proposicionales, se define
es un conjunto finito de variables
proposicionales, se define
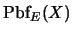 como sigue:
como sigue:
Sea 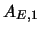 el sistema que consiste de los siguientes esquemas de axiomas:
el sistema que consiste de los siguientes esquemas de axiomas:
y sea 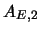 el sistema que consiste del siguiente esquema de axiomas:
el sistema que consiste del siguiente esquema de axiomas:
Considérese con cualquiera de estos sistemas la regla modus ponens como la única de inferencia.
Decida si el sistema 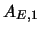 es equivalente al
es equivalente al 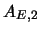 .
.
11. Muestre que todo teorema en el sistema 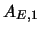 del ejercicio anterior es también un teorema en el sistema
del ejercicio anterior es también un teorema en el sistema
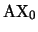 visto en clase.
visto en clase.
12. Considere el juego del AJEDREZ. Una configuración es cualquier manera de colocar las, o algunas, piezas del juego en el tablero del juego. Considere el sistema formal cuyo único axioma es la configuración inicial de cada partida y cuyas reglas de inferencia son precisamente las reglas del juego.
- Caracterice a los teoremas en AJEDREZ.
- Sea
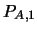 el conjunto de correspondencias que a cada casilla en el tablero le asocia una o ninguna pieza. Dé ejemplos de proposiciones en
el conjunto de correspondencias que a cada casilla en el tablero le asocia una o ninguna pieza. Dé ejemplos de proposiciones en 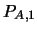 que no sean teoremas, es decir, que no sean deducibles en AJEDREZ.
que no sean teoremas, es decir, que no sean deducibles en AJEDREZ.
- Sea
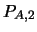 el conjunto de configuraciones que pueden aparecer en partidas legales. ¿Existen en este caso proposiciones que no sean deducibles?
el conjunto de configuraciones que pueden aparecer en partidas legales. ¿Existen en este caso proposiciones que no sean deducibles?
- Bosqueje un procedimiento para determinar si una configuración es o no un teorema.
13. Considere el CUBO DE RUBIK. Éste consta de 27 dados, los cuales dan 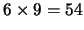 subcaras externas. Sea RUBIK el sistema formal cuyo único axioma es la configuración inicial del cubo, es decir aquella en la que las 9 subcaras de cada una de las 6 caras del cubo de Rubik tienen un mismo color, y cuyas reglas de inferencia están dadas por los movimientos legales del cubo de Rubik.
subcaras externas. Sea RUBIK el sistema formal cuyo único axioma es la configuración inicial del cubo, es decir aquella en la que las 9 subcaras de cada una de las 6 caras del cubo de Rubik tienen un mismo color, y cuyas reglas de inferencia están dadas por los movimientos legales del cubo de Rubik.
- Caracterice a los teoremas en RUBIK.
- Sea
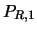 el conjunto de correspondencias que a cada subcara externa le asocia un color. Dé ejemplos de proposiciones en
el conjunto de correspondencias que a cada subcara externa le asocia un color. Dé ejemplos de proposiciones en 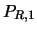 que no sean teoremas, es decir, que no sean deducibles en RUBIK.
que no sean teoremas, es decir, que no sean deducibles en RUBIK.
- Busque en un libro de álgebra o del cubo de Rubik la caracterización de un conjunto
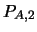 de configuraciones tal que todas las configuraciones en él sean deducibles.
de configuraciones tal que todas las configuraciones en él sean deducibles.
- Bosqueje un procedimiento para determinar si una configuración es o no un teorema (observe que se pide ``un procedimiento'', no ``un procedimiento óptimo'').
14. Considere el alfabeto que consta de dos símbolos 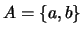 . Sea
. Sea 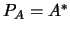 el diccionario de
el diccionario de  , es decir, el conjunto de todas las palabras de longitud finita sobre
, es decir, el conjunto de todas las palabras de longitud finita sobre  . Considere las siguientes dos reglas de inferencia:
. Considere las siguientes dos reglas de inferencia:
Considere como único axioma a la palabra 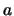 .
.
- Caracterice a los teoremas en ese sistema.
- Dé ejemplos de proposiciones en
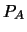 que no sean teoremas, es decir, que no sean deducibles en ese sistema.
que no sean teoremas, es decir, que no sean deducibles en ese sistema.
- Bosqueje un procedimiento para determinar si una palabra en
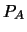 es o no un teorema.
es o no un teorema.
15. Definición formal de la conjunción. En el sistema formal
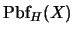 , con el conjunto de axiomas
, con el conjunto de axiomas
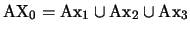 escribimos
escribimos
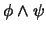 como una abreviatura de la proposición
como una abreviatura de la proposición
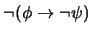 . Muestre que, cualesquiera que sean las proposiciones
. Muestre que, cualesquiera que sean las proposiciones  ,
, 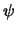 se tiene:
se tiene:
-
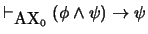
-
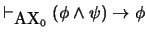
-
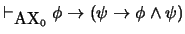
16. Definición formal de la disyunción. En el sistema formal
 , escribimos
, escribimos 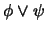 como una abreviatura de la proposición
como una abreviatura de la proposición
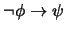 . Muestre que, cualesquiera que sean las proposiciones
. Muestre que, cualesquiera que sean las proposiciones  ,
, 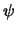 ,
, 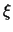 se tiene:
se tiene:
-
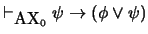
-
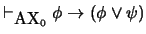
-
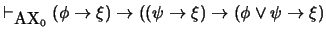
17. Muestre que si
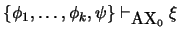 y también
y también
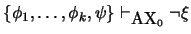 entonces necesariamente
entonces necesariamente
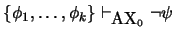 .
.
18. Muestre que para cualesquiera tres proposiciones  ,
, 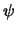 y
y 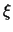 :
:
19. Recordamos que si 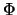 es un conjunto de proposiciones, entonces su teoría es
es un conjunto de proposiciones, entonces su teoría es
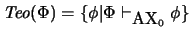 .
Muestre que
.
Muestre que
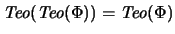 , cualquiera que sea
, cualquiera que sea 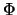 .
.
20. Un conjunto de proposiciones 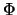 es inconsistente si existe una proposición
es inconsistente si existe una proposición  tal que
tal que
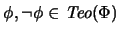 .
Muestre que
.
Muestre que 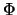 es inconsistente si y sólo si
es inconsistente si y sólo si
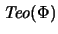 consta de todas las proposiciones ben formadas.
consta de todas las proposiciones ben formadas.



Posterior: Coherencia y completitud
Arriba: Cálculo proposicional
Anterior: Deducción natural
Guillermo Morales-Luna
2004-07-27