


Posterior: Ejercicios
Arriba: Sintaxis
Anterior: Reglas convencionales de buena
Los procedimientos de deducción natural se definen en el lenguaje
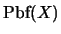 .
.
Definición 2.4 (Axiomas)
El conjunto de
AXIOMAS PROPOSICIONALES, sobre el conjunto de variables proposicionales
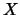
, es
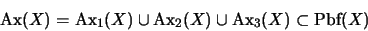 |
(5) |
donde
La regla MODUS PONENS (MP) se sintetiza como
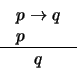 |
(9) |
y significa que toda vez que en una línea de razonamiento aparecen
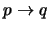 y
y 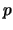 entonces se puede añadir
entonces se puede añadir 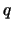 .
.
Definición 2.5 (Pruebas)
Sea

una colección de proposiciones bien formadas, llamadas
hipótesis. Una
PRUEBA es una sucesión finita
![$D=[p_1,\ldots,p_n]$](img1029.png)
de proposiciones bien formadas tal que
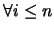
:
En este caso la prueba
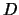
se dice ser una
prueba de 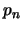 a partir de
a partir de 
.
Toda prueba 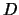 es entonces una sucesión finita de proposiciones bien formadas, es decir,
es entonces una sucesión finita de proposiciones bien formadas, es decir,
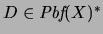 .
.
Definición 2.6 (Demostrabilidad)
Se dice que

es
DEMOSTRABLE a partir de

, y se escribe
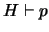
, si existe una prueba
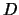
de
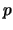
a partir de

.
El conjunto

de
DEDUCCIONES LÓGICAS de

es llamado también la
TEOR´i
A de

.
Una proposición
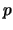
es un
TEOREMA si

, es decir, si
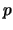
se deduce de los axiomas.
Ya que las pruebas son de longitud finita, necesariamente para cualquier
 se tiene
se tiene
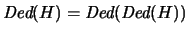 .
Ilustremos la noción de deducción lógica con algunos ejemplos.
.
Ilustremos la noción de deducción lógica con algunos ejemplos.
Demostración
A) Veamos que
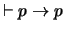 . Una prueba es la siguiente:
. Una prueba es la siguiente:
- 1.
-
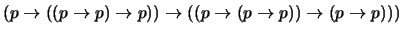 (
(
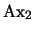 )
)
- 2.
-
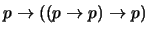 (
(
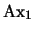 )
)
- 3.
-
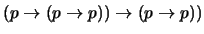 (
(
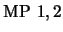 )
)
- 4.
-
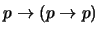 (
(
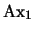 )
)
- 5.
-
 (
(
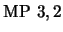 )
)
B) Veamos que
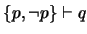 . Una prueba es la siguiente:
. Una prueba es la siguiente:
- 1.
-
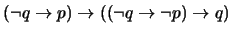 (
(
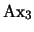 )
)
- 2.
-
 (
(
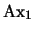 )
)
- 3.
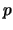 (
(
 )
)
- 4.
-
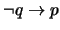 (
(
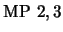 )
)
- 5.
-
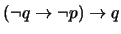 (
(
 )
)
- 6.
-
 (
(
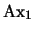 )
)
- 7.
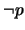 (
(
 )
)
- 8.
-
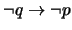 (
(
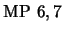 )
)
- 9.
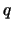 (
(
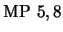 )
)
C) Veamos que
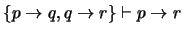 . Una prueba es la siguiente:
. Una prueba es la siguiente:
- 1.
-
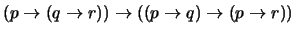 (
(
 )
)
- 2.
-
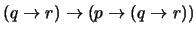 (
(
 )
)
- 3.
-
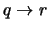 (
(
 )
)
- 4.
-
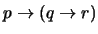 (
(
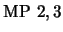 )
)
- 5.
-
 (
(
 )
)
- 6.
-
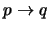 (
(
 )
)
- 7.
-
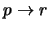 (
(
 )
)
D) Veamos que
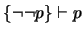 . Para esto hemos de calcar una prueba de la proposición
. Para esto hemos de calcar una prueba de la proposición
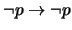 siguiendo el esquema en A) para continuar luego como sigue:
siguiendo el esquema en A) para continuar luego como sigue:
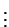
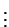 (
(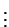 )
)
- 5.
-
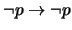 (
(
 )
)
- 6.
-
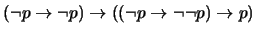 (
(
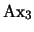 )
)
- 7.
-
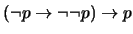 (
(
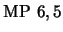 )
)
- 8.
-
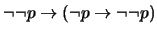 (
(
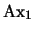 )
)
- 9.
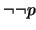 (
(
 )
)
- 10.
-
 (
(
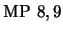 )
)
- 11.
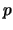 (
(
 )
)

Proposición 2.2
Para cualesquiera
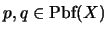
se cumple la siguiente relación:
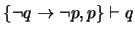
M
ODUS TOLLENS
Demostración
Una prueba es la siguiente:
- 1.
-
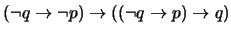 (
(
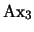 )
)
- 2.
-
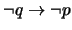 (
(
 )
)
- 3.
-
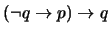 (
(
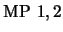 )
)
- 4.
-
 (
(
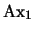 )
)
- 5.
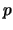 (
(
 )
)
- 6.
-
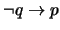 (
(
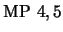 )
)
- 7.
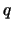 (
(
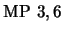 )
)
 Toda prueba puede ser vista como un árbol, que de hecho ha de ser binario en el cálculo proposicional, donde la raíz tiene como etiqueta el índice de la tesis en la prueba y las hojas tienen como etiquetas índices de axiomas o de hipótesis. Definiremos a los árboles de pruebas de manera inductiva.
Toda prueba puede ser vista como un árbol, que de hecho ha de ser binario en el cálculo proposicional, donde la raíz tiene como etiqueta el índice de la tesis en la prueba y las hojas tienen como etiquetas índices de axiomas o de hipótesis. Definiremos a los árboles de pruebas de manera inductiva.
Definición 2.7
Sea
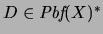
una prueba de longitud

. Y sea
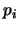
una proposición en
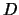
, con
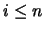
. La
SUBPRUEBA INDICADA de
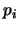
en
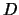
se define inductivamente en términos de cómo se haya obtenido
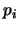
:
Caso base. Si
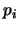
fuese un axioma o una hipótesis entonces
![$D_i=[(i:p_i)]$](img1093.png)
.
Caso inductivo. Si
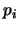
se obtiene de dos proposiciones previas por modus ponens, es decir, si existen
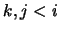
tales que
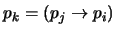
, entonces sean
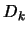
y
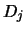
las correspondientes subpruebas indicadas de
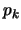
y

. Con ellas, se hace
![$D_i=D_k*D_j*[(i:p_i)]$](img1099.png)
, donde
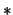
denota la operación de concatenación.
En otras palabras, la demostración indicada de una proposición 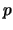 en una demostración dada
en una demostración dada 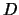 , consiste en extraer las proposiciones involucradas en demostrar
, consiste en extraer las proposiciones involucradas en demostrar 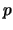 , enumerándolas con los mismos números asignados por
, enumerándolas con los mismos números asignados por 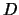 .
.
Definición 2.8
Sea
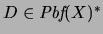
una prueba de longitud

. Definimos inductivamente en términos de

a
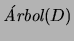
:
Caso base. Si

entonces
![$D=[p_1]$](img1102.png)
y
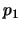
es un axioma o es una hipótesis. En tal caso
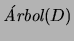
consta de un único nodo raíz con etiqueta
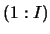
donde
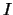
es el tipo de axioma, si
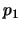
fuese un axioma, o bien

, si
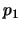
fuese una hipótesis.
Caso inductivo. Si
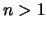
entonces
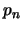
se obtiene por modus ponens de dos proposiciones previas
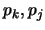
:
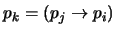
. En tal caso, sean
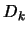
y
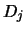
las correspondientes subpruebas indicadas de
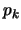
y

.
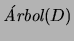
será entonces el árbol cuya raíz tiene etiqueta
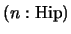
, y cuyos subárboles izquierdo y derecho son
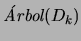
y
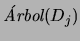
, respectivamente.
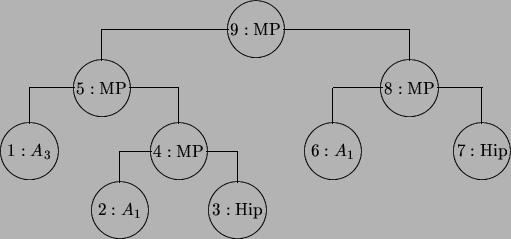
Ejemplo 2.3
Consideremos las fórmulas de la proposición
2.2.1. En la figura
2.3 presentamos el árbol del teorema en

). En la figura
2.4 presentamos el árbol de la deducción en

).
Observamos en estos caso que la ``tesis'' corresponde a la raíz y los axiomas o las hipótesis a las hojas. Los árboles son binarios porque la regla de modus ponens es la única que se aplica y ésta involucra a exactamente dos proposiciones.
Figure 2.3:
Árbol de demostración del teorema
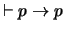 .
.
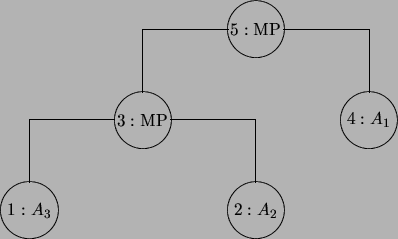 |
Figure 2.4:
Árbol de demostración de la deducción
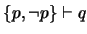 .
.
 |
De los ejemplos vistos, queda la impresión de que el proceso de deducción mostrado, llamado por algunos autores DEDUCCIÓN NATURAL, es, precisamente ``poco natural'', en el sentido de que el hallazgo de una prueba puede ser difícil. El siguiente teorema permite transformar pruebas en otras pruebas, de manera algorítmica. Este es un importante teorema en la lógica matemática.
Teorema 2.1 (de la deducción
(Hildebrand, 1930))
Sea

un conjunto de proposiciones bien formadas y sean
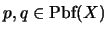
otras dos proposiciones. Entonces:
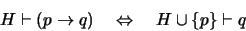 |
(10) |
De hecho, la demostración del teorema de la deducción permite transformar algorítmicamente una prueba de
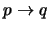 a partir de
a partir de  en una prueba de
en una prueba de 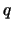 a partir de
a partir de 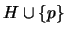 , y viceversa.
Demostración
, y viceversa.
Demostración
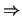 ) Supongamos que
) Supongamos que 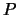 es una sucesión de
es una sucesión de  proposiciones que forma una prueba de
proposiciones que forma una prueba de
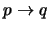 a partir de
a partir de  . Entonces, al concatenarle las siguientes dos proposiciones obtenemos una prueba de
. Entonces, al concatenarle las siguientes dos proposiciones obtenemos una prueba de 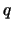 a partir de
a partir de 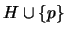 :
:
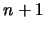 .
.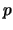 (
(
 )
)
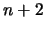 .
.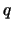 (
(
 )
)
 ) Supongamos que
) Supongamos que 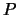 es una sucesión de
es una sucesión de  proposiciones que forma una prueba de
proposiciones que forma una prueba de 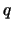 a partir de
a partir de 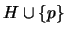 . Razonando por inducción en
. Razonando por inducción en  construiremos una prueba de
construiremos una prueba de
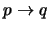 a partir de
a partir de  .
.
Caso base. Si  entonces
entonces 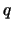 es bien un axioma o una hipótesis, es decir, pertenece a
es bien un axioma o una hipótesis, es decir, pertenece a 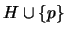 . Si
. Si  entonces
entonces
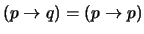 es un teorema (véase el ejemplo A) en la proposición 2.2.1 anterior). En otro caso, una prueba de
es un teorema (véase el ejemplo A) en la proposición 2.2.1 anterior). En otro caso, una prueba de
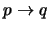 a partir de
a partir de  es la siguiente:
es la siguiente:
- 1.
-
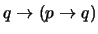 (
(
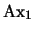 )
)
- 2.
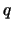 (
(
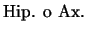 )
)
- 3.
-
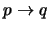 (
(
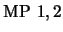 )
)
Caso inductivo. Supongamos 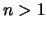 y, de acuerdo con el Principio de Inducción, que la equivalencia (10) vale cuando las pruebas requieren menos de
y, de acuerdo con el Principio de Inducción, que la equivalencia (10) vale cuando las pruebas requieren menos de  pasos.
Comp
pasos.
Comp  es una prueba de
es una prueba de  a partir de
a partir de 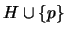 con exactamente
con exactamente  pasos, la última justificación en esa prueba debe ser Modus Ponens. Así pues para algunos pasos
pasos, la última justificación en esa prueba debe ser Modus Ponens. Así pues para algunos pasos  las correspondientes proposiciones han de ser de la forma
las correspondientes proposiciones han de ser de la forma
 y
y 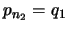 . Por la hipótesis de inducción se tiene que existe una prueba
. Por la hipótesis de inducción se tiene que existe una prueba 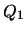 de que
de que
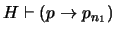 y una prueba
y una prueba  de que
de que
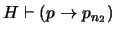 , digamos que de
, digamos que de 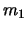 y
y 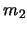 pasos. La concatenación de
pasos. La concatenación de 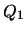 y
y  con los siguientes pasos da una prueba de
con los siguientes pasos da una prueba de
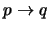 a partir de
a partir de  :
:
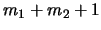 .
.-
 (
(
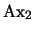 )
)
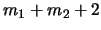 .
.-
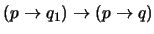 (
(
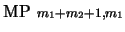 )
)
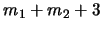 .
.-
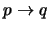 (
(
 )
)
 Siguiendo esta demostración, el lector no tendrá problema alguno para precisar un algoritmo recursivo que tome como entrada la prueba
Siguiendo esta demostración, el lector no tendrá problema alguno para precisar un algoritmo recursivo que tome como entrada la prueba 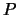 de una proposición
de una proposición 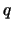 a partir de
a partir de 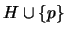 , y produzca como salida una prueba
, y produzca como salida una prueba  de
de
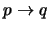 a partir de
a partir de  .
Aplicando el Teorema de la Deducción a las deducciones hechas en la proposición 2.2.1, obtenemos inmediatamente:
.
Aplicando el Teorema de la Deducción a las deducciones hechas en la proposición 2.2.1, obtenemos inmediatamente:
Proposición 2.3
Para cualesquiera
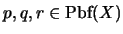
las siguientes proposiciones son teoremas:
Demostración
Sólo demostraremos el enunciado 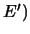 pues los anteriores se siguen inmediatamente.
De
pues los anteriores se siguen inmediatamente.
De 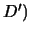 se tiene que
se tiene que
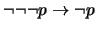 es un teorema. Utilizando este hecho y el Teorema de Deducción, basta probar
es un teorema. Utilizando este hecho y el Teorema de Deducción, basta probar
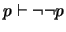 . Procedamos como sigue:
. Procedamos como sigue:
- 1.
-
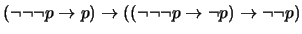 (
(
 )
)
- 2.
-
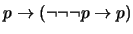 (
(
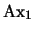 )
)
- 3.
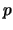 (
(
 )
)
- 4.
-
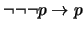 (
(
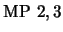 )
)
- 5.
-
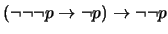 (
(
 )
)
- 6.
-
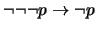 (
(
 )
)
- 7.
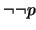 (
(
 )
)

Proposición 2.4
Para cualesquiera
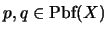
se cumple la siguiente relación:
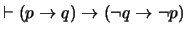
P
RINCIPIO DE C
ONTRAPOSICIÓN
Demostración
En efecto, por Modus Tollens,
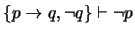 . Luego, por el Teorema de Deducción,
. Luego, por el Teorema de Deducción,
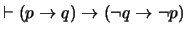 .
.  Para concluir esta sección presentaremos la noción de consistencia formal.
Para concluir esta sección presentaremos la noción de consistencia formal.
Definición 2.9
Un conjunto

se dice ser
FORMALMENTE INCONSISTENTE si existe una proposición

tal que
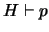
y
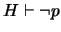
.
El conjunto

es
FORMALMENTE CONSISTENTE si no es inconsistente, vale decir, si vale que
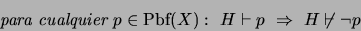 |
(11) |
Naturalmente se tiene la siguiente
Proposición 2.5
Sea

. Entonces
 |
(12) |
Demostración
 Supongamos
Supongamos  formalmente inconsistente. Sea
formalmente inconsistente. Sea
 tal que
tal que 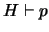 y
y
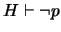 . Sea ahora
. Sea ahora
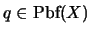 una proposición cualquiera. Veamos que
una proposición cualquiera. Veamos que 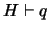 . En efecto, una prueba es la siguiente:
. En efecto, una prueba es la siguiente:
- 1.
-
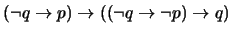 (
(
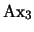 )
)
- 2.
-
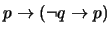 (
(
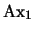 )
)
- 3.
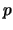 (
(
 )
)
- 4.
-
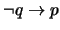 (
(
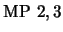 )
)
- 5.
-
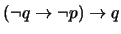 (
(
 )
)
- 6.
-
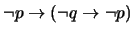 (
(
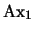 )
)
- 7.
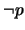 (
(
 )
)
- 8.
-
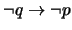 (
(
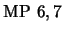 )
)
- 9.
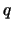 (
(
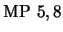 )
)
 Supongamos que
Supongamos que
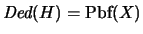 . Entonces para cualquier
. Entonces para cualquier
 se tiene que
se tiene que 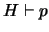 y además
y además
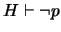 , es decir,
, es decir,  es formalmente inconsistente.
es formalmente inconsistente.
 Un criterio para decidir cuándo un conjunto de proposiciones de inconsistente lo da el siguiente
Un criterio para decidir cuándo un conjunto de proposiciones de inconsistente lo da el siguiente
Teorema 2.2 (de Compacidad)
Un conjunto (acaso infinito) de proposiciones

es consistente si y sólo si cualquier subconjunto finito de él lo es. En otras palabras,

es inconsistente si y sólo si posee un subconjunto finito que en sí es inconsistente.
La demostración es directa y se debe únicamente a que las pruebas involucran sólo un número finito de proposiciones. 



Posterior: Ejercicios
Arriba: Sintaxis
Anterior: Reglas convencionales de buena
Guillermo Morales-Luna
2004-07-27