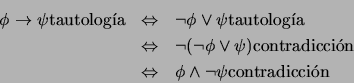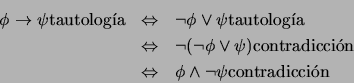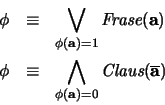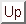


Posterior: Tablas de verdad
Arriba: Procedimientos de demostración automática
Anterior: Procedimientos de demostración automática
Observamos que se cumple cada una de las equivalencias lógicas siguientes:
En consecuencia:
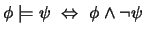 es una
contradicción.
O, equivalentemente:
es una
contradicción.
O, equivalentemente:
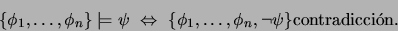 |
(1) |
La equivalencia (1) determina el PRINCIPIO DE PRUEBA POR
REFUTACIÓN: Para demostrar
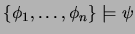 es
suficiente demostrar que
es
suficiente demostrar que
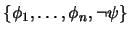 es un conjunto contradictorio de proposiciones.
Ahora bien, recordamos que para cada proposición
es un conjunto contradictorio de proposiciones.
Ahora bien, recordamos que para cada proposición  se cumplen las siguientes dos equivalencias:
se cumplen las siguientes dos equivalencias:
En los métodos de demostración automática que presentaremos en esta sección, consideraremos únicamente el problema de decidir la satisfactibilidad de formas conjuntivas, FC's.
Dada una cláusula
reenumeramos a sus componentes, colocando primero las literales que aparezcan negadas. Obtenemos
Por las Leyes de De Morgan, tendremos
y como
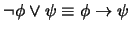 :
:
Con esta notación escribimos:
Así, una cláusula
![$\mbox{\bf c} = [ F ; C ]$](img1338.png) se ha de leer como
se ha de leer como
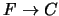 , donde
, donde 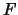 es la lista izquierda cuyos elementos están conectados por conjunciones, en tanto que
es la lista izquierda cuyos elementos están conectados por conjunciones, en tanto que 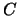 es la lista derecha cuyos elementos están conectados por disyunciones. En particular:
es la lista derecha cuyos elementos están conectados por disyunciones. En particular:
-
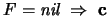 es equivalente a la
cláusula
es equivalente a la
cláusula 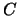 .
.
-
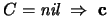 es equivalente a la
negación de la frase
es equivalente a la
negación de la frase 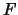 .
.
Una proposición  escrita en FC queda pues como una lista de cláusulas
escrita en FC queda pues como una lista de cláusulas
![$\phi = ( [ F_i ; C_i ] )_i.$](img1342.png) Las cláusulas se sobreentienden conectadas por conjunciones.
Recordamos que
Las cláusulas se sobreentienden conectadas por conjunciones.
Recordamos que
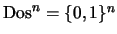 consta de las listas de 0's y 1's de longitud
consta de las listas de 0's y 1's de longitud 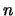 .
Éstas representan en binario a los números enteros entre 0 y
.
Éstas representan en binario a los números enteros entre 0 y 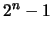 inclusive. Tal representación es, de hecho, una enumeración de
inclusive. Tal representación es, de hecho, una enumeración de
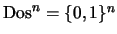 .
Después de estos preliminares, pasemos a ver diversos algoritmos para decidir cuándo un conjunto dado de proposiciones es o no contradictorio.
.
Después de estos preliminares, pasemos a ver diversos algoritmos para decidir cuándo un conjunto dado de proposiciones es o no contradictorio.



Posterior: Tablas de verdad
Arriba: Procedimientos de demostración automática
Anterior: Procedimientos de demostración automática
Guillermo Morales-Luna
2004-07-27