Entrada:
Salida:
Algoritmo: Dada una proposición
- Si es ``
 '', entonces
'', entonces  es de la forma
es de la forma
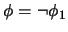 .
En este caso, revise si
.
En este caso, revise si 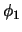 posee conectivos. Si los tuviese,
transforme
posee conectivos. Si los tuviese,
transforme  en
en 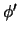 según las fórmulas
según las fórmulas
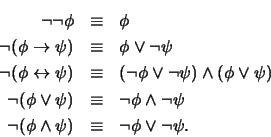
Si no los tuviese y
y 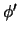 coinciden
Haga
coinciden
Haga
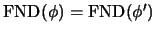 .
.
- Si es ``
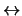 '' o ``
'' o ``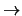 '' transforme
'' transforme  a
una proposición equivalente
a
una proposición equivalente 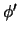 en términos de
en términos de
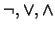 , según las fórmulas
, según las fórmulas
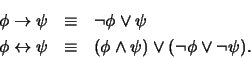
En este caso,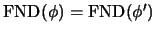 .
.
- Si es ``
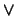 '' entonces
'' entonces  es de la forma
es de la forma
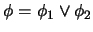 .
En este caso,
.
En este caso,
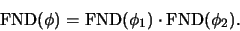
- Si es ``
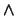 '' entonces
'' entonces  es de la forma
es de la forma
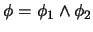 .
En este caso, calcúlese
.
En este caso, calcúlese
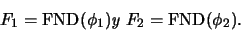
Concatenemos cada frase en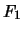 con cada frase en
con cada frase en 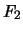 . En
cada una de las frases obtenidas eliminemos literales repetidas.
Sea
. En
cada una de las frases obtenidas eliminemos literales repetidas.
Sea 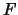 la lista que se obtiene de todas esas frases eliminando
repeticiones de frases. Tendremos que
la lista que se obtiene de todas esas frases eliminando
repeticiones de frases. Tendremos que
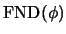 es la lista
es la lista
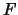 reducida.
reducida.
- Si no hubiera conectivos, entonces
 ha de ser una variable
proposicional
ha de ser una variable
proposicional 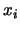 .
En este caso,
.
En este caso,
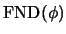 es la lista consistente de la única
frase cuya única literal es
es la lista consistente de la única
frase cuya única literal es  misma.
misma.