Entrada:
Salida:
Algoritmo:
- Coloque al inicio de
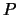 una proposición
que no sea una literal.
una proposición
que no sea una literal.
- Sea
 esta proposición y sea
esta proposición y sea 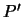 el resto de
el resto de 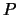 .
.
- Transforme
 a una proposición equivalente, sólo con
conectivos
a una proposición equivalente, sólo con
conectivos
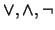 .
.
- Revise el conectivo principal de
 :
:
- Si éste es
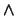 , entonces
, entonces
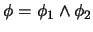 . Sustituya
a
. Sustituya
a 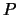 por la lista
por la lista
![$[\phi_1, \phi_2] * P'$](img1385.png) (donde
(donde 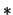 es la
concatenación de listas). Invoque a este mismo algoritmo con la
sustitución hecha. Si obtiene una respuesta afirmativa
es la
concatenación de listas). Invoque a este mismo algoritmo con la
sustitución hecha. Si obtiene una respuesta afirmativa 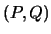 es
una tautología.
es
una tautología.
- Si éste es
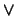 , entonces
, entonces
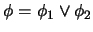 . Invoque este
mismo algoritmo, una vez con el argumento
. Invoque este
mismo algoritmo, una vez con el argumento
![$([\phi_1] * P' , Q)$](img1387.png) y otra con
el argumento
y otra con
el argumento
![$([\phi_2] * P' , Q)$](img1388.png) .
Si en ambos casos obtiene una respuesta afirmativa entonces
.
Si en ambos casos obtiene una respuesta afirmativa entonces 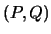 es una tautología.
es una tautología.
- Si éste es
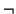 , entonces
, entonces
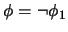 . Invoque este mismo
algoritmo, con el argumento
. Invoque este mismo
algoritmo, con el argumento
![$(P, [\phi_1] * Q)$](img1389.png) . Si obtiene una
respuesta afirmativa entonces
. Si obtiene una
respuesta afirmativa entonces 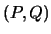 es una tautología.
es una tautología.
- Si éste es
- Si todas las proposiciones en
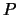 son literales, considere ahora
a
son literales, considere ahora
a 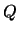 .
.
- Sea
- Coloque al inicio de
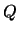 una proposición que no sea una
literal.
una proposición que no sea una
literal.
- Sea
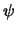 esta proposición y sea
esta proposición y sea 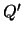 el resto de
el resto de 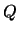 .
.
- Transforme
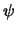 a una proposición equivalente, sólo con
conectivos
a una proposición equivalente, sólo con
conectivos
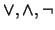 .
.
- Revise el conectivo principal de
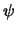 .
.
- Si éste es
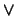 , entonces
, entonces
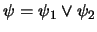 . Sustituya a
. Sustituya a
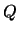 por la lista
por la lista
![$[\psi_1,\psi_2] * Q'$](img1392.png) . Invoque a este mismo algoritmo
con la sustitución hecha. Si obtiene una respuesta afirmativa
. Invoque a este mismo algoritmo
con la sustitución hecha. Si obtiene una respuesta afirmativa
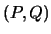 es una tautología.
es una tautología.
- Si éste es
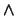 , entonces
, entonces
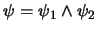 . Invoque
este mismo algoritmo, una vez con el argumento
. Invoque
este mismo algoritmo, una vez con el argumento
![$(P, [\psi_1] * Q')$](img1394.png) y
otra con el argumento
y
otra con el argumento
![$(P, [\psi_2] * Q')$](img1395.png) . Si en ambos casos obtiene
una respuesta afirmativa
. Si en ambos casos obtiene
una respuesta afirmativa 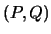 es una tautología.
es una tautología.
- Si éste es
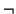 , entonces
, entonces
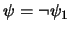 . Invoque este mismo
algoritmo, con el argumento
. Invoque este mismo
algoritmo, con el argumento
![$([\psi_1] * P, Q')$](img1397.png) . Si obtiene una
respuesta afirmativa entonces
. Si obtiene una
respuesta afirmativa entonces 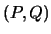 es una tautología.
es una tautología.
- Si éste es
- Si todas las proposiciones en
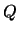 también son literales, continúe con el paso siguiente.
también son literales, continúe con el paso siguiente.
- Sea
- Vea si acaso hay una literal común a
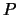 y a
y a 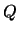 .
.
- En este caso
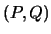 es una tautología.
es una tautología.
- En caso contrario, no lo es, de hecho al hacer
a las literales en
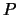 verdaderas y a las literales en
verdaderas y a las literales en 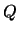 falsas
obtenemos una asignación que hace a
falsas
obtenemos una asignación que hace a 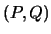 falsa.
falsa.
- En este caso
- En un inicio, si se da una proposición
 , al invocar el
algoritmo con el argumento
, al invocar el
algoritmo con el argumento
![$(\mbox{\it nil},[\phi])$](img1398.png) , donde
, donde
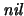 es
la lista vacía, entonces el algoritmo descrito nos dice si
es
la lista vacía, entonces el algoritmo descrito nos dice si  es o no una tautología.
es o no una tautología.