Entrada:
Salida:
Algoritmo:
- Literales aisladas contradictorias: Si para una misma literal
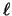 , tanto
, tanto 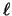 como
como 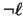 aparecen como literales aisladas,
aparecen como literales aisladas,  es una contradicción.
es una contradicción.
- Literales aisladas: Si
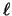 aparece aislada pero
aparece aislada pero 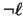 no, hagamos
no, hagamos

Sea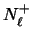 el conjunto consistente de
el conjunto consistente de 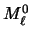 junto con el
conjunto de cláusulas que se obtiene de
junto con el
conjunto de cláusulas que se obtiene de 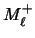 suprimiendo toda
aparición de
suprimiendo toda
aparición de 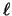 . Similarmente, sea
. Similarmente, sea 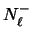 el conjunto consistente
de
el conjunto consistente
de 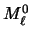 junto con el conjunto de cláusulas que se obtiene
de
junto con el conjunto de cláusulas que se obtiene
de 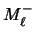 suprimiendo toda aparición de
suprimiendo toda aparición de 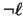 .
Entonces
.
Entonces 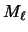 es contradicción si y sólo si
es contradicción si y sólo si 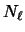 es
contradicción.
es
contradicción.
- Literales puras: Si
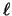 es una literal que aparece pura
entonces
es una literal que aparece pura
entonces  es contradicción si y sólo si
es contradicción si y sólo si 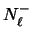 es contradicción,
donde
es contradicción,
donde 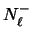 está definida como en la regla anterior.
está definida como en la regla anterior.
- Bifurcación: Para una literal cualquiera
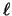 , tendremos que
, tendremos que
 es contradicción si y sólo si ambos conjuntos de clásulas
es contradicción si y sólo si ambos conjuntos de clásulas
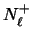 y
y 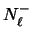 son contradicciones.
son contradicciones.