


Posterior: Programas
Arriba: Procedimientos de demostración automática
Anterior: Algoritmo de Davis y
Se tiene que las siguientes aseveraciones son siempre verdaderas:
-
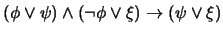 es una tautología.
es una tautología.
-
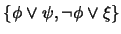 es Consistente
es Consistente
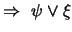 es Consistente.
es Consistente.
- Principio de Resolución.
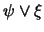 es contradicción
es contradicción
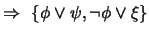 es contradicción
es contradicción
Sobre este algoritmo, formulamos las siguientes observaciones:
- Es no-determinista pues la elección de
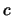 en el punto 1. no está precisada.
en el punto 1. no está precisada.
- Si el algoritmo da como resultado el valor nil, entonces en efecto
 es insatisfactible.
es insatisfactible.
- Si el algoritmo da como resultado el valor Indefinido, entonces no necesariamente hemos de tener que
 es satisfactible. Tan solo podemos concluir que la búsqueda realizada ha fracasado en probar que
es satisfactible. Tan solo podemos concluir que la búsqueda realizada ha fracasado en probar que 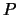 es insatisfactible.
es insatisfactible.



Posterior: Programas
Arriba: Procedimientos de demostración automática
Anterior: Algoritmo de Davis y
Guillermo Morales-Luna
2004-07-27