Posterior: About this document ... Arriba: Cálculo proposicional Anterior: Resolución lineal

Programas

1. Algoritmo de Quine-McCluskey. Escriba un programa que dado un conjunto 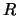$R$ de vértices en el hipercubo 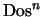$\mbox{\rm Dos}^n$, lo exprese como una unión mínima de subcubos maximales.

2. Escriba un programa que evalúe formas booleanas con la representación de asignaciones introducida en la sección 2.1.4 (vea la página 24 del texto).

3. Analizador sintáctico de proposiciones de enfijo. Escriba un programa que revise que una cadena de caracteres sea una proposición, escrita en notación de enfijo, bien formada. Y en caso de que lo sea, haga una lista de las variables proposicionales que involucra.

4. Analizador sintáctico de proposiciones de prefijo. Escriba un programa que revise que una cadena de caracteres sea una proposición, escrita en notación de prefijo, bien formada, en la que pueden aparecer los cuatro conectivos booleanos: 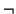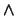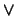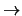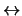$\neg$, $\land$, $\lor$, $\rightarrow$, $\leftrightarrow$. Y en caso de que lo sea, haga una lista de las variables proposicionales que involucra.

5. Convertidor de proposiciones de enfijo a prefijo. Escriba un programa que reciba una proposición, escrita en notación de enfijo, y la transforme en su proposición equivalente, escrita en notación de prefijo.

6. Convertidor de proposiciones de prefijo a enfijo. Escriba un programa que reciba una proposición, escrita en notación de prefijo, y la transforme en su proposición equivalente, escrita en notación de enfijo.

7. Convertidor de proposiciones de prefijo a proposiciones de deducción natural. Escriba un programa que reciba una proposición, escrita en notación de prefijo, en la que pueden aparecer los cuatro conectivos booleanos: 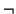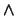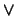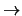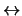$\neg$, $\land$, $\lor$, $\rightarrow$, $\leftrightarrow$, y la transforme en su proposición equivalente, escrita en notación de prefijo del tipo de deducción natural en la que sólo aparecer los conectivos booleanos: 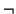$\neg$ y $\rightarrow$.

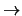8. Revisor de pruebas. Escriba un programa que reciba una sucesión finita de proposiciones de deducción natural, es decir, en 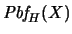$\mbox{\it Pbf}_H(X)$ y decida si esa sucesión es o no una prueba de su última proposición.

9. Teorema de Deducción. Escriba un programa que reciba una prueba de 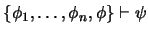$\{\phi_1,\ldots,\phi_n,\phi\} \vdash \psi$ y que la transforme, utilizando el Teorema de Deducción, en una prueba de $\{\phi_1,\ldots,\phi_n\} \vdash \phi\rightarrow \psi$.

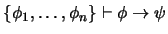10. Lema previo al Teorema de Completitud. Escriba un programa que reciba una asignación 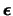$\mbox{\boldmath$\epsilon$}$ y una proposición 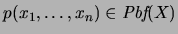$p(x_1,\ldots,x_n)\in\mbox{\it Pbf}(X)$ y constuya un aprueba de que 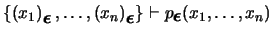$\left\{\left(x_1\right)_{\mbox{\boldmath$\epsilon$}}, \ldots, \left(x_n\right)_... ...math$\epsilon$}} \right\} \vdash p_{\mbox{\boldmath$\epsilon$}}(x_1,\ldots,x_n)$, siguiendo el esquema en la demostración de la proposición 2.3.1.

11. Teorema de Completitud. Escriba un programa que reciba una tautología y escriba una demostración de ella. Sugerencia. Puede emplear los dos programas anterioes en esat lista.

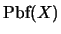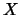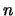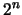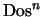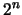12. Evaluación de tablas de verdad. Escriba un programa que dada una proposición $\phi$ en $\mbox{\rm Pbf}(X)$, decida cuántos elementos tiene $X$, si tiene $n$ entonces enumere a las $2^n$ asignaciones en $\mbox{\rm Dos}^n$ y para cada una de ellas calcule el valor de verdad que le asigna a $\phi$. la salida del programa ha de ser una lista de $2^n$ valores de verdad.

13. Escriba un programa que implemente el algoritmo Encadenamiento hacia atrás de la sección 2.4.3.

14. Escriba un programa que decida si una proposición es satisfactible mediante el algoritmo de la sección 2.4.4.

15. Escriba un programa que decida si una proposición es refutable mediante el algoritmo de la sección 2.4.4.

16. Escriba un programa que calcule la forma normal conjuntiva de cualquier proposición mediante el algoritmo de la sección 2.4.5.

17. Escriba un programa que calcule la forma normal disyuntiva de cualquier proposición mediante el algoritmo de la sección 2.4.5.

18. Escriba un programa que decida si una proposición es satisfactible mediante el algoritmo de Wang, visto en la sección 2.4.7.

19. Escriba un programa que dada la forma normal conjuntiva de una proposición la transforme en la forma normal disyuntiva equivalente; y que dada la forma normal disyuntiva de una proposición la transforme en la forma normal conjuntiva equivalente.

20. Escriba un programa que decida si una proposición es satisfactible mediante el algoritmo de representación matricial, visto en la sección 2.4.8.

21. Escriba un programa que decida si una proposición es satisfactible mediante el algoritmo de Davis y Putnam, visto en la sección 2.4.9.

22. Escriba un programa que decida si una proposición es satisfactible mediante el algoritmo de resolución lineal, visto en la sección 2.4.10.
Posterior: About this document ... Arriba: Cálculo proposicional Anterior: Resolución lineal