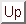


Posterior: Retículos Arriba: Estructuras algebraicas
básicas Anterior: Estructuras algebraicas básicas
Definición 1.1 Sea

un
conjunto no vacío y sea ``
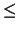
''
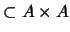
una relación.
Se dice que
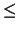
es un
ORDEN,
o una
RELACIÓN DE ORDEN, si
cumple con las siguientes propiedades:
- Reflexividad:
-
 .
.
- Transitividad:
-
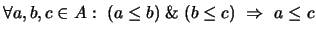 .
.
- Antisimetría:
-
 .
.
En tal caso la estructura
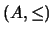
se dice ser un
CONJUNTO
ORDENADO.
La relación ``
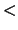
'' tal que:

,
se dice ser el
ORDEN ESTRICTO inducido
por
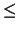
.
Si además se cumple la propiedad:
- Tricotomía:
-
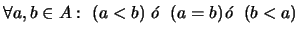 .
.
entonces el orden se dice ser
LINEAL o
TOTAL.
Algunos autores suelen llamar ORDEN PARCIAL
a todo orden que no sea total. Así que aquí hemos de
considerar sólo órdenes parciales a menos de que
explícitamente indiquemos que se trata de órdenes
totales, cuando nos refiramos a tales órdenes.
Ejemplo 1.1 Sea
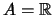
y sea
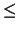
el orden usual
de
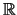
.
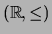
es un orden total.
En efecto, un número real distinto de 0 cuya parte entera es un
número natural se dice ser positivo y un número
real cuyo inverso aditivo es positivo se dice ser negativo.
Así tenemos que todo real o bien es negativo o es cero o es
positivo. Para cualesquiera dos reales 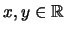 se tiene:
se tiene:  no es negativo. Esta
relación es un orden total.
no es negativo. Esta
relación es un orden total. 
Evidentemente, si 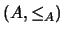 es ordenado y
es ordenado y 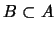 es un subconjunto de
es un subconjunto de  , entonces
, entonces 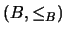 es ordenado, donde
es ordenado, donde
 se dice ser el ORDEN HEREDADO o INDUCIDO por
se dice ser el ORDEN HEREDADO o INDUCIDO por 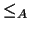 en
en  . Así, por ejemplo, los
conjuntos de números naturales, enteros y racionales
. Así, por ejemplo, los
conjuntos de números naturales, enteros y racionales 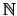 ,
,  y
y 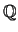 respectivamente, son ordenados con los
correspondientes órdenes inducidos por el orden usual de
respectivamente, son ordenados con los
correspondientes órdenes inducidos por el orden usual de 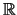 .
.
Definición 1.2 Sean

y
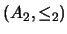
dos conjuntos
ordenados. El
ORDEN PRODUCTO es la
relación definida en el producto cartesiano
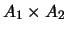
siguiente:
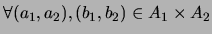
,
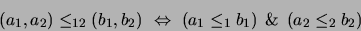 |
(1) |
Resulta que 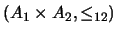 es, en efecto, un conjunto ordenado.
es, en efecto, un conjunto ordenado.
Ejemplo 1.2 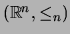
, donde
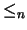
es la
potencia

-ésima del orden usual de
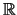
, es un conjunto ordenado.
Explícitamente, se tiene:

Ejemplo 1.3 (Algebra de conjuntos) Sea

un conjunto no vacío, y sea
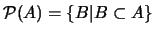
su
CONJUNTO DE PARTES. Entonces
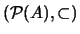
es un conjunto ordenado
![[*]](footnote.png)
.
Ejemplo 1.4 (Divisibilidad) Sea
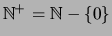
el conjunto de
números naturales positivos. Para
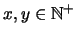
decimos que
 DIVIDE
DIVIDE a

, y escribimos
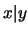
, si
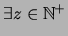
:

.
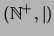
es un conjunto ordenado.
Ejemplo 1.5 (Gráficas dirigidas) Sea
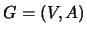
una gráfica dirigida, sin ciclos. En el
conjunto de vértices, digamos que
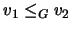
si es
que hay un camino en

que se inicia en

y
llega a
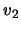
.

es un
conjunto ordenado, que se dice ser
DETERMINADO por

.
Sea 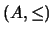 un conjunto ordenado y sean
un conjunto ordenado y sean 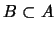 y
y  un subconjunto y un elemento
de
un subconjunto y un elemento
de  respectivamente.
respectivamente.
 es una COTA SUPERIOR de
es una COTA SUPERIOR de 
- si
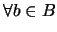 :
: 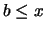 .
.
 es una COTA INFERIOR de
es una COTA INFERIOR de 
- si
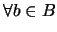 :
: 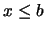 .
.
 es un elemento MAXIMAL de
es un elemento MAXIMAL de 
- si
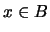 y no hay elemento en
y no hay elemento en  que lo
supere:
que lo
supere: 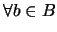 ,
, 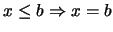 .
.
 es un elemento MINIMAL de
es un elemento MINIMAL de 
- si
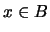 y no hay elemento en
y no hay elemento en  por
debajo de él:
por
debajo de él: 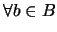 ,
, 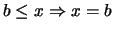 .
.
 es el MÁXIMO de
es el MÁXIMO de 
- si
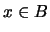 y es una cota superior de
y es una cota superior de  .
.
 es el M´iNIMO de
es el M´iNIMO de 
- si
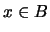 y es una cota inferior de
y es una cota inferior de  .
.
 es el SUPREMO
de
es el SUPREMO
de 
- si
 es la mínima de las cotas superiores
de
es la mínima de las cotas superiores
de  .
.
 es el íNFIMO de
es el íNFIMO de 
- si
 es la máxima de las cotas inferiores
de
es la máxima de las cotas inferiores
de  .
.
De estas definiciones, se sigue inmediatamente que si sólo hay
un elemento maximal entonces ése ha de ser un máximo. Si
hay más de un elemento maximal entonces no existirá un
máximo. Si un máximo existe, entonces ése ha de
ser un supremo. Sin embargo, puede haber supremos aunque no existan
máximos. Los correspondientes enunciados duales también
se siguen inmdediatamente.
Para un elemento 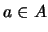 el CONO SUPERIOR de
el CONO SUPERIOR de 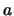 es
es 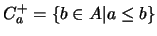 , y el CONO INFERIOR de
, y el CONO INFERIOR de 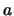 es
es 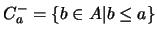 . Los elementos SUCESORES de
. Los elementos SUCESORES de 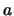 son los minimales del conjunto
son los minimales del conjunto 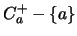 y los elementos ANTECESORES de
y los elementos ANTECESORES de 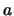 son los maximales del conjunto
son los maximales del conjunto 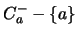 .
.
El conjunto ordenado 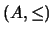 se dice ser DISCRETO si todo elemento en él o es maximal o el cono
superior de ese elemento es la unión de los conos de sus
sucesores.
se dice ser DISCRETO si todo elemento en él o es maximal o el cono
superior de ese elemento es la unión de los conos de sus
sucesores.
Para ilustrar las nociones anteriores, consideremos el conjunto
ordenado 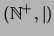 . El número 1 es un
mínimo y no hay máximos. Para un número
. El número 1 es un
mínimo y no hay máximos. Para un número  dado, el cono superior consta de sus múltiplos y el
cono inferior de sus divisores. El supremo del conjunto formado por dos
números es su mínimo común múltiplo y su
ínfimo es su máximo común divisor. Los sucesores
del número 1 son los números primos. Un sucesor de un
número
dado, el cono superior consta de sus múltiplos y el
cono inferior de sus divisores. El supremo del conjunto formado por dos
números es su mínimo común múltiplo y su
ínfimo es su máximo común divisor. Los sucesores
del número 1 son los números primos. Un sucesor de un
número  es de la forma
es de la forma 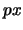 donde
donde 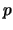 es un primo, y un antecesor es de la forma
es un primo, y un antecesor es de la forma  donde
donde 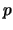 es un primo que divida a
es un primo que divida a  .
.
Definición 1.3 Sea
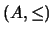
un conjunto ordenado discreto. Su
DIAGRAMA
es la gráfica dirigida

donde

consta
de los arcos que unen a elementos con sus sucesores:

,
Naturalmente, 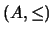 coincide con el orden determinado por
su propio diagrama.
coincide con el orden determinado por
su propio diagrama.



Posterior: Retículos Arriba: Estructuras algebraicas
básicas Anterior: Estructuras algebraicas básicas
Guillermo
Morales-Luna
2004-07-27
 .
. 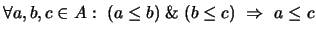 .
. .
.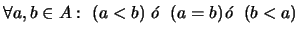 .
.![[*]](footnote.png) .
.