


Posterior: Modelo constructible de la
Arriba: Teoría de conjuntos
Anterior: Teoría de conjuntos
Para construir este modelo, supondremos la existencia de los números ordinales. Recordamos que un ORDINAL es un conjunto TRANSITIVO, es decir, un conjunto  tal que
tal que
que además está BIEN ORDENADO bajo la relación 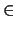 , es decir, para cualquier subconjunto
, es decir, para cualquier subconjunto 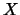 de
de  existe un elemento
existe un elemento 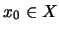 tal que para todo
tal que para todo 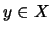 tal que
tal que 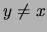 se tiene
se tiene 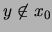 (es decir,
(es decir, 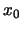 es un punto
es un punto 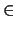 -minimal de
-minimal de 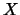 ).
Sea pues
).
Sea pues
 la clase de números ordinales. Se tiene que para cualquier ordinal
la clase de números ordinales. Se tiene que para cualquier ordinal
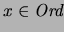 se cumple sólo una de las siguientes tres aseveraciones:
se cumple sólo una de las siguientes tres aseveraciones:
 coincide con el conjunto vacío, es decir,
coincide con el conjunto vacío, es decir,  es el primer ordinal:
es el primer ordinal: 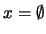 .
.
 es el sucesor de un ordinal:
es el sucesor de un ordinal:
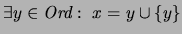 .
.
 es un ordinal límite:
es un ordinal límite:
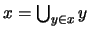 .
.
En la tabla 3.2 enlistamos algunos de los ``primeros'' ordinales.
Table 3.2:
Primeros ordinales (hasta el primer ordinal no-numerable).
|
|
Definición 2.5
La
JERARQU´i
A ACUMULATIVA DE CONJUNTOS es la sucesión
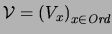
definida como sigue:
Se tiene que 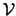 es una interpretación de todos los axiomas que determinan a la Teoría de Conjuntos de Zermelo-Fraenkel. Esta interpretación se llama ESTÁNDAR de la teoría de conjuntos.
De hecho, si denotamos por
es una interpretación de todos los axiomas que determinan a la Teoría de Conjuntos de Zermelo-Fraenkel. Esta interpretación se llama ESTÁNDAR de la teoría de conjuntos.
De hecho, si denotamos por 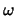 al primer ordinal límite, es decir,
al primer ordinal límite, es decir, 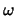 es el orden del conjunto de los números naturales, entonces
es el orden del conjunto de los números naturales, entonces 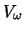 es un conjunto de todos los axiomas de Zermelo-Fraenkel exceptuando al exioma de infinito.
es un conjunto de todos los axiomas de Zermelo-Fraenkel exceptuando al exioma de infinito. 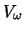 es pues un modelo donde todos los conjuntos son finitos.
es pues un modelo donde todos los conjuntos son finitos.



Posterior: Modelo constructible de la
Arriba: Teoría de conjuntos
Anterior: Teoría de conjuntos
Guillermo Morales-Luna
2004-07-27