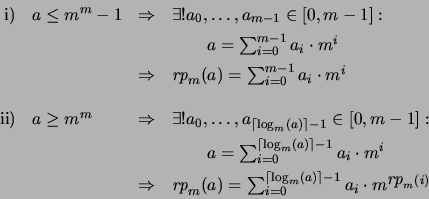Posterior: Sucesión de Goodstein
Arriba: El teorema de Goodstein
Anterior: El teorema de Goodstein
Sea 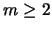 . Para cada
. Para cada 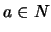 definimos
definimos
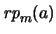 como sigue:
como sigue:
Ejemplo 5.4
Para
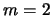
y
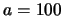
tenemos
luego
Escribamos
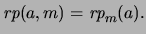 Con esta notación denotaremos por
Con esta notación denotaremos por
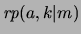 al resultado de sustituir a
al resultado de sustituir a 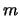 por
por 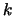 en
en
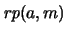 .
.
Guillermo Morales-Luna
2004-07-27