


Posterior: Cuaterniones
Arriba: Campos algebraicos
Anterior: Campos algebraicos
Sea
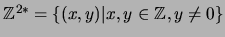 el conjunto de parejas de enteros cuyas segundas componentes no son cero. Si
el conjunto de parejas de enteros cuyas segundas componentes no son cero. Si
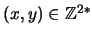 , a la primera componente
, a la primera componente  se le llama NUMERADOR y a la segunda,
se le llama NUMERADOR y a la segunda, 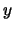 , DENOMINADOR. En
, DENOMINADOR. En
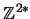 se introduce la relación de equivalencia:
se introduce la relación de equivalencia:
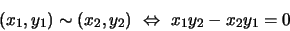 |
(1) |
y al espacio cociente
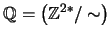 se le llama el conjunto de números RACIONALES. A cada elemento, que es en sí una clase de equivalencia,
se le llama el conjunto de números RACIONALES. A cada elemento, que es en sí una clase de equivalencia,
![$\left[(x,y)\right]$](img359.png) se le suele escribir
se le suele escribir 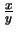 , o bien
, o bien 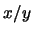 . Evidentemente,
. Evidentemente,
| |
|
![$\displaystyle \forall \left[(x,y)\right]\in{\mathbb{Q}}\,\exists x_1,y_1\in{\mathbb{Z}}:$](img362.png) |
|
| |
|
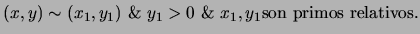 |
(2) |
(evidentemente, si
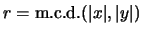 entonces hagamos
entonces hagamos 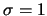 si ambos
si ambos  ,
, 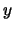 poseen el mismo signo,
poseen el mismo signo, 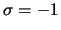 si
si  ,
, 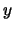 poseen signo distinto,
poseen signo distinto,
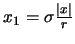 e
e
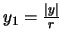 .) La pareja
.) La pareja
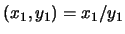 se dice ser el representante reducido del racional
se dice ser el representante reducido del racional
![$\left[(x,y)\right]$](img359.png) . En lo que sigue, representaremos a cada racional por su representante reducido.
Sea
. En lo que sigue, representaremos a cada racional por su representante reducido.
Sea
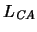 el alfabeto de la teoría de campos algebraicos. Se construye una interpretación
el alfabeto de la teoría de campos algebraicos. Se construye una interpretación
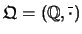 como sigue:
Al símbolo
como sigue:
Al símbolo 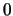 se le asocia el racional
se le asocia el racional
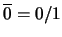 .
Al símbolo
.
Al símbolo 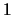 se le asocia el racional
se le asocia el racional
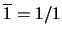 .
A
.
A 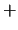 se le asocia la función
se le asocia la función
A 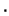 se le asocia la función
se le asocia la función
A 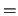 se le asocia la relación de equivalencia
se le asocia la relación de equivalencia 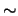 :
:
Puede verse que en 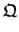 se satisfacen todos los axiomas de campos. Incluso más: este campo es conmutativo, es decir,
se satisfacen todos los axiomas de campos. Incluso más: este campo es conmutativo, es decir,
y es ARQUIMEDIANO, es decir,



Posterior: Cuaterniones
Arriba: Campos algebraicos
Anterior: Campos algebraicos
Guillermo Morales-Luna
2004-07-27