Posterior: Enteros módulo-
Arriba: Campos algebraicos
Anterior: Números racionales
El conjunto de CUATERNIONES coincide con el espacio real de 4 dimensiones. Sea
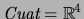 . Si
. Si
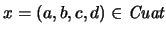 es un cuaternión, lo escribiremos como
es un cuaternión, lo escribiremos como 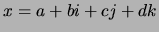 , y diremos que el cuaternión
, y diremos que el cuaternión
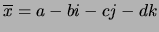 es su CONJUGADO. Los números
es su CONJUGADO. Los números 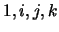 se dicen ser BÁSICOS
La suma de cuaterniones se define ``entrada-a-entrada'':
se dicen ser BÁSICOS
La suma de cuaterniones se define ``entrada-a-entrada'':
En cuanto al producto, definimos primeramente sobre los básicos las relaciones siguientes:
luego, extendemos por distributividad este producto a todo
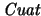 . De hecho, se ha de tener:
. De hecho, se ha de tener:
donde la expresión en el segundo miembro de esta igualdad se evalúa según las reglas del cálculo matricial.
Se tiene, naturalmente, que el inverso aditivo de cualquier cuaternión 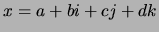 es
es
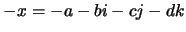 . Ahora, si
. Ahora, si 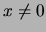 entonces al multiplicarlo por su conjugado, se obtiene:
entonces al multiplicarlo por su conjugado, se obtiene:
así pues
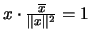 . En consecuencia, el inverso multiplicativo de
. En consecuencia, el inverso multiplicativo de  es, precisamente,
es, precisamente,
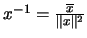 .
.
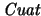 es entonces un campo y por ende una
es entonces un campo y por ende una
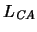 -estructura. con la interpretación construída como sigue:
Al símbolo
-estructura. con la interpretación construída como sigue:
Al símbolo 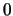 se le asocia el cuaternión
se le asocia el cuaternión
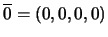 .
Al símbolo
.
Al símbolo 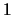 se le asocia el cuaternión
se le asocia el cuaternión
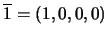 .
A
.
A 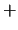 se le asocia la función suma definida por la ec. (3).
A
se le asocia la función suma definida por la ec. (3).
A 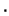 se le asocia la función producto definida por la ec. (4).
A
se le asocia la función producto definida por la ec. (4).
A 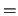 se le asocia la relación de igualdad de
se le asocia la relación de igualdad de
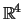 :
:
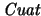 es un campo que no es conmutativo, aunque sí es arquimediano.
es un campo que no es conmutativo, aunque sí es arquimediano.
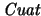 contiene a los campos usuales de números reales y de números complejos: El campo de los números reales se identifica con el subconjunto
contiene a los campos usuales de números reales y de números complejos: El campo de los números reales se identifica con el subconjunto
 y el campo de los números complejosa con el subconjunto
y el campo de los números complejosa con el subconjunto
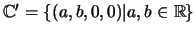 .
.



Posterior: Enteros módulo-
Arriba: Campos algebraicos
Anterior: Números racionales
Guillermo Morales-Luna
2004-07-27