 |
![[*]](footnote.png) . Un conjunto
difuso es también una función que asocia a cada
objeto del universo un valor en el intervalo
. Un conjunto
difuso es también una función que asocia a cada
objeto del universo un valor en el intervalo ![[*]](footnote.png) sets. En
español no hay una tal convención, así que
aquí los llamaremos sencillamente conjuntos usuales.
El conjunto vacío
sets. En
español no hay una tal convención, así que
aquí los llamaremos sencillamente conjuntos usuales.
El conjunto vacío  |
![[*]](footnote.png)
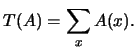 El peso relativo,
respecto a
El peso relativo,
respecto a
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
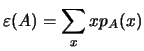 . Inclusive,
se define la noción de
. Inclusive,
se define la noción de 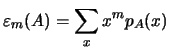 . Los
momentos de un conjunto difuso proporcionan información sobre la
``distribución'' de los puntos en ese conjunto difuso.
. Los
momentos de un conjunto difuso proporcionan información sobre la
``distribución'' de los puntos en ese conjunto difuso.
|
![[*]](footnote.png) en tanto que si para
cada
en tanto que si para
cada
|
|
|