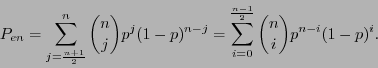Siguiente: Distancia de Hamming
Arriba: Códigos binarios
Anterior: Códigos binarios
Código por mayoría de votos
Supongamos que se quiere transmitir mensajes, desde una parte emisora a una receptora, por un canal que comete errores con una distribución binomial, es decir, existe un ![$p\in[0,1]$](img238.png) tal que para cada
tal que para cada
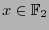 , si
, si 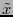 es el valor recibido a través del canal, entonces la probabilidad de error es
es el valor recibido a través del canal, entonces la probabilidad de error es
Como un primer paso para detectar errores se podría utilizar, para un número
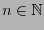 impar, el código
impar, el código
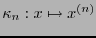 , que codifica cada bit
, que codifica cada bit 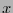 mediante
mediante  repeticiones consecutivas de él mismo. En la parte del receptor, para decodificar un bloque
repeticiones consecutivas de él mismo. En la parte del receptor, para decodificar un bloque 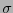 de
de  bits, se procede por simple mayoría: el valor
bits, se procede por simple mayoría: el valor 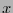 que aparezca más veces en
que aparezca más veces en 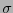 es el que se toma como transmitido.
es el que se toma como transmitido.
La probabilidad de cometer un error en la decodificación es la probabilidad de que habiendo transmitido un bit 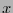 , su valor complementario sea mayoritario en
, su valor complementario sea mayoritario en 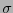 . Así pues ésta es:
. Así pues ésta es:
Para 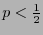 se tiene
se tiene 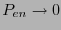 conforme
conforme  aumenta de tamaño; para
aumenta de tamaño; para 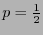 se tiene
se tiene
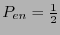 independientemente del valor de
independientemente del valor de  ; pero para
; pero para 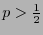 se tiene
se tiene 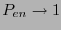 conforme
conforme  aumenta de tamaño.
aumenta de tamaño.




Siguiente: Distancia de Hamming
Arriba: Códigos binarios
Anterior: Códigos binarios
Guillermo M. Luna
2010-05-09
![]() tal que para cada
tal que para cada
![]() , si
, si ![]() es el valor recibido a través del canal, entonces la probabilidad de error es
es el valor recibido a través del canal, entonces la probabilidad de error es
![]() , su valor complementario sea mayoritario en
, su valor complementario sea mayoritario en ![]() . Así pues ésta es:
. Así pues ésta es: