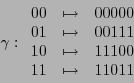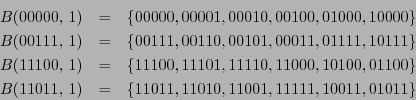Siguiente: Códigos lineales: Códigos rectangulares
Arriba: Códigos binarios
Anterior: Código por mayoría de
Para
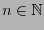 hay
hay 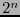 palabras de longitud
palabras de longitud  con símbolos
con símbolos 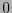 ,
, 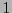 . Sea
. Sea
![$k\in[\![1,n]\!]$](img256.png) y sea
y sea
![$K\subset[\![0,n-1]\!]$](img257.png) un conjunto de índices de cardinalidad
un conjunto de índices de cardinalidad 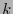 . Sea
. Sea
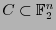 un conjunto de cardinalidad
un conjunto de cardinalidad 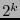 y sea
y sea
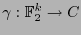 tal que existe
tal que existe
![$\iota:[\![0,k-1]\!]\to K$](img261.png) biyectiva, con la condición:
biyectiva, con la condición:
Se dice que el código 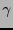 posee
posee 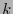 bits de información y utiliza
bits de información y utiliza 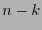 bits de revisión. El cociente
bits de revisión. El cociente
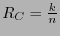 es la razón de información del código
es la razón de información del código  .
.
Por ejemplo, para el código por mayoría de votos visto en la sección anterior 4.1,  es un número impar,
es un número impar, 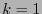 y, por ejemplo,
y, por ejemplo, 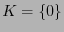 .
. 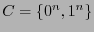 y
y
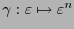 . Entonces ese código tiene un solo bit de información, utiliza
. Entonces ese código tiene un solo bit de información, utiliza 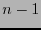 bits de revisión y su razón de información es
bits de revisión y su razón de información es 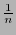 .
.
Ejemplo 4.1
Sea
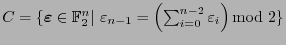 el conjunto de palabras cuyo último símbolo es la paridad del bloque formado por los primeros
el conjunto de palabras cuyo último símbolo es la paridad del bloque formado por los primeros 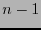 . Para
. Para 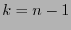 y
y
![$K=[\![0,n-2]\!]$](img273.png) , las funciones
, las funciones 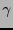 e
e 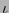 quedan determinadas naturalmente:
quedan determinadas naturalmente:
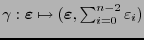 ,
,
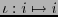 . Entonces
. Entonces 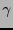 es un código con
es un código con 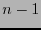 bits de información y
bits de información y 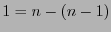 bit de revisión. La razón de información de este código es
bit de revisión. La razón de información de este código es 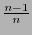 .
.
Observemos que en el ejemplo anterior, cualesquiera dos palabras en el código  difieren en por lo menos 3 bits. Así pues, habiendo recibido una palabra
difieren en por lo menos 3 bits. Así pues, habiendo recibido una palabra
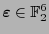 , si ésta no está en
, si ésta no está en  se reconoce que hay un error.
se reconoce que hay un error.
Las palabras con error pueden ser complementarias de palabras de código o las restantes (éstas son
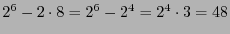 ) y para cada una de estas últimas habrá una única palabra
) y para cada una de estas últimas habrá una única palabra
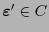 que difiera de
que difiera de
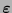 en tan solo un bit. Se toma entonces a la palabra correspondiente con
en tan solo un bit. Se toma entonces a la palabra correspondiente con
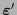 según
según 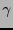 y de esta manera se corrige el error. (Para cada palabra complementaria de una palabra de código hay tres palabras de código que difieren de ella en dos bits.)
y de esta manera se corrige el error. (Para cada palabra complementaria de una palabra de código hay tres palabras de código que difieren de ella en dos bits.)
Definición 4.1 (Distancia de Hamming)
Sea
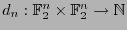 ,
la función que a cada par de palabras le asocia el número de sus discordancias.
Naturalmente,
,
la función que a cada par de palabras le asocia el número de sus discordancias.
Naturalmente, 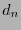 es una función distancia en
es una función distancia en
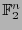 , llamada de Hamming.
, llamada de Hamming.
Definición 4.2
Para cada
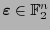 y
y
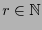 la esfera de radio
la esfera de radio 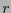 centrada en
centrada en
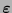 es
y la bola de radio
es
y la bola de radio 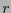 centrada en
centrada en
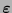 es
es
Así, se tiene que
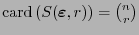 y
y
![$\mbox{\rm card}\,(B(\mbox{\boldmath$\varepsilon$},r)) = \sum_{s\in[\![0,r]\!]}{n\choose s}$](img301.png) .
.
Definición 4.3
Para un punto
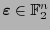 y un conjunto
y un conjunto
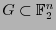 se define
se define
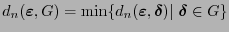 . Para dos conjuntos
. Para dos conjuntos
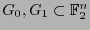 se define
se define
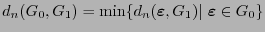 .
.
Definición 4.4
Para un conjunto
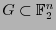 su diámetro es
Su distancia mínima es
su diámetro es
Su distancia mínima es
Observación 4.1
Para cualquier código
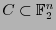 tal que
tal que
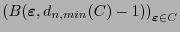 sea un recubrimiento de
sea un recubrimiento de
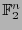 se tiene
se tiene
 reconoce
reconoce 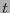 errores si y sólo si
errores si y sólo si
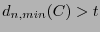
 corrige
corrige 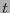 errores si y sólo si
errores si y sólo si
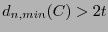
En efecto, para la primera aseveración: Supóngase que se quiere enviar la palabra
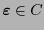 y se recibe
y se recibe
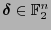 . Entonces pueden ocurrir dos casos. Si
. Entonces pueden ocurrir dos casos. Si
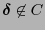 , se habrá detectado un error y como éste está en una bola de radio
, se habrá detectado un error y como éste está en una bola de radio
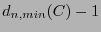 con centro en un punto de
con centro en un punto de  se ve que hay menos de
se ve que hay menos de 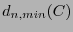 errores. Si, por lo contrario,
errores. Si, por lo contrario,
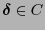 , entonces bien
, entonces bien
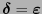 , en cuyo caso no hay error, o bien
, en cuyo caso no hay error, o bien
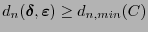 y no será posible detectar los más de
y no será posible detectar los más de 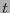 errores cometidos.
errores cometidos.
La segunda aseveración se sigue de lo siguiente: Supóngase que se quiere enviar la palabra
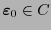 y se recibe
y se recibe
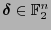 con a lo sumo
con a lo sumo 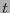 errores. Entonces
errores. Entonces
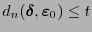 . Sea
. Sea
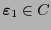 una palabra en el código, distinta de la enviada. Entonces
una palabra en el código, distinta de la enviada. Entonces
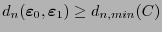 . Resulta pues
. Resulta pues
Por tanto:
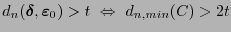 .
. 
Definición 4.5
Un código
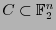 con
con 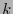 bits de información y
bits de información y 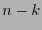 bits de revisión se dice ser un código-
bits de revisión se dice ser un código-![$[n,k]$](img326.png) . En este caso se dice también que
. En este caso se dice también que 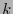 es la dimensión de
es la dimensión de  y que
y que  es su longitud.
Todo código-
es su longitud.
Todo código-![$[n,k]$](img326.png) de distancia mínima
de distancia mínima 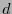 se dice ser un código-
se dice ser un código-![$[n,k,d]$](img328.png) .
.
La observación 4.1 se reformula como la siguiente:
Por la observación 4.2, se tiene que puede corregir un solo bit. Alrededor de cada palabra de código, la bola de radio 1 consiste de
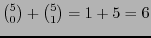 elementos. Se tiene;
elementos. Se tiene;
Estas bolas son ajenas a pares y su unión consiste de 24 palabras. Las restantes 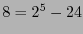 equidistan en 2 de dos palabras de código.
equidistan en 2 de dos palabras de código. 




Siguiente: Códigos lineales: Códigos rectangulares
Arriba: Códigos binarios
Anterior: Código por mayoría de
Guillermo M. Luna
2010-05-09
![]() hay
hay ![]() palabras de longitud
palabras de longitud ![]() con símbolos
con símbolos ![]() ,
, ![]() . Sea
. Sea
![]() y sea
y sea
![]() un conjunto de índices de cardinalidad
un conjunto de índices de cardinalidad ![]() . Sea
. Sea
![]() un conjunto de cardinalidad
un conjunto de cardinalidad ![]() y sea
y sea
![]() tal que existe
tal que existe
![]() biyectiva, con la condición:
biyectiva, con la condición:
![]() es un número impar,
es un número impar, ![]() y, por ejemplo,
y, por ejemplo, ![]() .
. ![]() y
y
![]() . Entonces ese código tiene un solo bit de información, utiliza
. Entonces ese código tiene un solo bit de información, utiliza ![]() bits de revisión y su razón de información es
bits de revisión y su razón de información es ![]() .
.

![]() ) y para cada una de estas últimas habrá una única palabra
) y para cada una de estas últimas habrá una única palabra
![]() que difiera de
que difiera de
![]() en tan solo un bit. Se toma entonces a la palabra correspondiente con
en tan solo un bit. Se toma entonces a la palabra correspondiente con
![]() según
según ![]() y de esta manera se corrige el error. (Para cada palabra complementaria de una palabra de código hay tres palabras de código que difieren de ella en dos bits.)
y de esta manera se corrige el error. (Para cada palabra complementaria de una palabra de código hay tres palabras de código que difieren de ella en dos bits.)
![]() y se recibe
y se recibe
![]() con a lo sumo
con a lo sumo ![]() errores. Entonces
errores. Entonces
![]() . Sea
. Sea
![]() una palabra en el código, distinta de la enviada. Entonces
una palabra en el código, distinta de la enviada. Entonces
![]() . Resulta pues
. Resulta pues