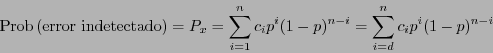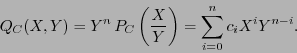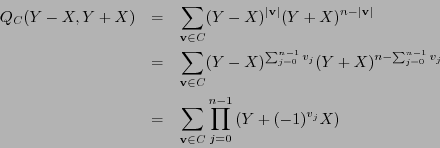Siguiente: Códigos lineales
Arriba: Códigos binarios
Anterior: Distancia de Hamming
Definición 4.6
Un código
 se dice ser lineal si posee al origen y es cerrado bajo la suma de
se dice ser lineal si posee al origen y es cerrado bajo la suma de
 .
.
En el caso de un código lineal, el peso de cualquier palabra
 es
es
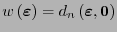 , y el peso mínimo del código es
, y el peso mínimo del código es
Observación 4.3
Para cualquier código lineal
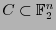 se tiene
se tiene
 reconoce
reconoce 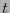 errores si
errores si 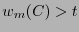
 corrige
corrige 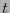 errores si
errores si 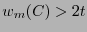
Puede verse que  es un código lineal, pues contiene al origen y es cerrado bajo la suma. Si un elemento
es un código lineal, pues contiene al origen y es cerrado bajo la suma. Si un elemento
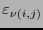 toma el valor
toma el valor  , entonces debe aparecer un
, entonces debe aparecer un  en otra posición en la misma columna y un
en otra posición en la misma columna y un  también en otra posición en el mismo renglón, y debe haber un
también en otra posición en el mismo renglón, y debe haber un  en la esquina opuesta a
en la esquina opuesta a 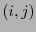 . En consecuencia, el peso mínimo de
. En consecuencia, el peso mínimo de  es
es 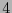 y por tanto es capaz de detectar hasta 3 errores.
y por tanto es capaz de detectar hasta 3 errores.
Se tiene que un vector
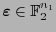 estará en el código si y sólo si se satisfacen las
estará en el código si y sólo si se satisfacen las 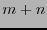 ecuaciones
ecuaciones
Todo código lineal es un subespacio lineal de
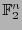 y por tanto ha de poseer una base. Cualquier palabra podrá ser escrita como una combinación lineal de los elementos en la base y por tanto las palabras en el código han de satisfacer un conjunto de ecuaciones lineales tal como en el caso de los códigos rectangulares.
y por tanto ha de poseer una base. Cualquier palabra podrá ser escrita como una combinación lineal de los elementos en la base y por tanto las palabras en el código han de satisfacer un conjunto de ecuaciones lineales tal como en el caso de los códigos rectangulares.
En efecto, si un código lineal  es de dimensión
es de dimensión 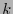 en
en
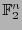 , sea
, sea
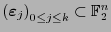 una base de
una base de  . La matriz
. La matriz
![$H =\left[\mbox{\boldmath$\varepsilon$}_j\right]_{0\leq j\leq k}\in \mathbb{F}_2^{n\times k}$](img362.png) que posee como columnas a los vectores básicos, llamada generatriz de
que posee como columnas a los vectores básicos, llamada generatriz de  , es de orden
, es de orden 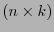 y determina un isomorfismo
y determina un isomorfismo
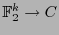 ,
,
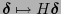 . Existe entonces una matriz
. Existe entonces una matriz
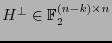 tal que
tal que
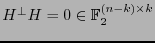 . Así se ha de tener la equivalencia:
. Así se ha de tener la equivalencia:
![$\left[\mbox{\boldmath$\varepsilon$}\in C\ \Leftrightarrow\ H^{\perp}\mbox{\boldmath$\varepsilon$}={\bf0}\right]$](img368.png) . La matriz
. La matriz 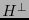 se dice ser una revisora de paridad del código
se dice ser una revisora de paridad del código  .
.
Proposición 4.1
Un código  corrige errores de un bit si y sólo si cualquier matriz revisora de paridad suya posee columnas no-nulas y distintas a pares.
corrige errores de un bit si y sólo si cualquier matriz revisora de paridad suya posee columnas no-nulas y distintas a pares.
Sea
![${\bf e}_j=\left[\delta_{ij}\right] _{i=0}^{n-1}$](img370.png) el
el 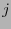 -ésimo vector de la base canónica,
-ésimo vector de la base canónica,
 . Denotemos también por
. Denotemos también por
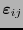 al vector que coincide con
al vector que coincide con 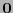 salvo que en sus dos entradas
salvo que en sus dos entradas  y
y 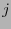 posee el valor 1,
posee el valor 1,
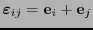 .
.
La proposición se sigue de que las siguientes aseveraciones son equivalentes a pares:
 corrige errores de un bit.
corrige errores de un bit.
- El peso mínimo de
 es al menos 3.
es al menos 3.
- Ninguno de los vectores
 ,
,
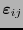 puede estar en
puede estar en  .
.
- Para cada
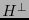 revisora de paridad, los productos
revisora de paridad, los productos
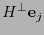 ,
,
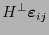 no pueden ser nulos.
no pueden ser nulos.
- Para cada
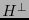 revisora de paridad, las columnas de
revisora de paridad, las columnas de 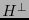 son no-nulas y distintas a pares.
son no-nulas y distintas a pares.
Definición 4.7
Para cada 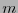 , sea
, sea
![$H_m^{\perp}=\left[\mbox{\boldmath$\varepsilon$}\right]_{\mbox{\scriptsize\boldm...
...n\mathbb{F}_2^{m}-\{\mbox{\bf\scriptsize0}\}} \in\mathbb{F}_2^{m\times (2^m-1)}$](img380.png) la matriz cuyas columnas son los vectores no-nulos en
la matriz cuyas columnas son los vectores no-nulos en
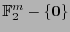 . Todo código que posea a
. Todo código que posea a 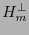 como matriz revisora de paridad se dice ser de Hamming1.
como matriz revisora de paridad se dice ser de Hamming1.
Así todo código de Hamming posee
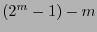 bits de información y
bits de información y 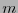 bits de revisión, y su razón de información es
bits de revisión, y su razón de información es
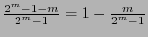 .
.
La matriz 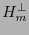 queda determinada de manera única salvo el orden en el que se enumere a los elementos de
queda determinada de manera única salvo el orden en el que se enumere a los elementos de
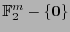 . Sea
. Sea
![$\kappa_m:[\![1,2^m-1]\!]\to[\![1,2^m-1]\!]$](img385.png) la permutación que ordena a los índices de acuerdo con el peso de Hamming y en orden lexicográfico cuando haya coincidencia de pesos. Por ejemplo:
la permutación que ordena a los índices de acuerdo con el peso de Hamming y en orden lexicográfico cuando haya coincidencia de pesos. Por ejemplo:
 .
.-

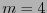 .
.-
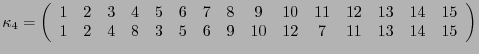
Si a los índices se les ordena de acuerdo con 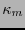 , entonces se podrá escribir
, entonces se podrá escribir
![$H_m^{\perp} = \left[I_m\ G_m\right]$](img391.png) donde
donde  es la matriz identidad de orden
es la matriz identidad de orden 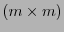 y
y  es una matriz de orden
es una matriz de orden
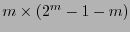 . Así pues, se tendrá que una palabra
. Así pues, se tendrá que una palabra
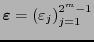 está en el código de Hamming si y sólo si
está en el código de Hamming si y sólo si
![$\left[I_m\ G_m\right]\,\kappa_m(\mbox{\boldmath$\varepsilon$}) = {\bf0}$](img397.png) , donde
, donde
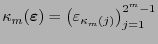 , lo cual equivale a que
, lo cual equivale a que
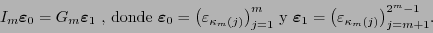 |
(7) |
El conjunto de índices
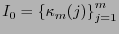 corresponde a los bits de revisión y el conjunto
corresponde a los bits de revisión y el conjunto
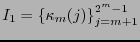 a los de información.
a los de información.
Sea
![$H_m=\left[\begin{array}{c} G_m \\ I_{2^m-1-m}\end{array}\right]\in\mathbb{F}_2^{\left(2^m-1\right)\times\left(2^m-1-m\right)}$](img402.png) . Entonces,
. Entonces,
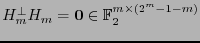 y por tanto las columnas de
y por tanto las columnas de 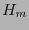 forman una base del código de Hamming. La dimensión del código es el número de bits de información, a saber,
forman una base del código de Hamming. La dimensión del código es el número de bits de información, a saber,  .
.
Para codificar una palabra
![${\bf\delta}=\left[\delta_j\right]_{j=1}^{2^m-1-m}\in\mathbb{F}_2^{2^m-1-m}$](img406.png) se construye
se construye
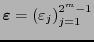 haciendo
haciendo
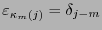 para
para
![$j\in[\![m+1,2^m-1]\!]$](img408.png) y, para
y, para
![$j\in[\![1,m]\!]$](img409.png) , los valores
, los valores
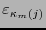 quedan determinados por la ec. (7).
quedan determinados por la ec. (7).
Para decodificar un
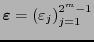 , se revisa si éste está en el código. El vector
, se revisa si éste está en el código. El vector
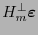 se dice ser el síndrome de
se dice ser el síndrome de
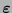 . Si el síndrome fuese nulo no se hace ninguna corrección y se recupera
. Si el síndrome fuese nulo no se hace ninguna corrección y se recupera
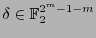 mediante los bits de información:
mediante los bits de información:
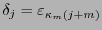 , para
, para
![$j\in[\![1,2^m-1-m]\!]$](img414.png) . En otro caso, deben existir
. En otro caso, deben existir
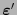 en el código de Hamming y un índice
en el código de Hamming y un índice
![$i\in[\![1,2^m-1]\!]$](img415.png) tales que
tales que
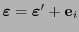 . Por tanto, ha de tenerse
. Por tanto, ha de tenerse
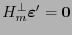 y
y
y la  -ésima columna de
-ésima columna de 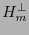 no es otra que la representación en base 2 del índice
no es otra que la representación en base 2 del índice  . Así pues, el síndrome indica cuál es el índice que ha de conmutarse para corregir el error.
. Así pues, el síndrome indica cuál es el índice que ha de conmutarse para corregir el error.
En efecto, si la matriz revisora de paridad se escribe como las representaciones en base 2 de los números en
![$[\![1,2^m-1]\!]$](img419.png) , entonces las tres primeras columnas, correspondientes a 1, 2 y 3 forman una submatriz
, entonces las tres primeras columnas, correspondientes a 1, 2 y 3 forman una submatriz 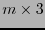 con un bloque inicial de
con un bloque inicial de 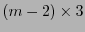 ceros y los dos últimos renglones son
ceros y los dos últimos renglones son
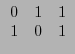 . De aquí se ve que la palabra
. De aquí se ve que la palabra
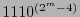 está en el código. Por tanto
está en el código. Por tanto
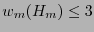 . Por otro lado, como el código corrige un bit, por la observación 4.1, se tiene que
. Por otro lado, como el código corrige un bit, por la observación 4.1, se tiene que
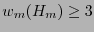 .
. 
Observación 4.5
Los códigos de Hamming son perfectos en el sentido de que cualquier palabra en el espacio que contiene a las palabras de código, es bien una palabra de código o bien dista en  de una palabra de código.
de una palabra de código.
Definición 4.8
Supongamos que
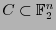 es un código lineal con palabras de código de longitud
es un código lineal con palabras de código de longitud 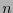 , y que un canal binario simétrico, con probabilidad
, y que un canal binario simétrico, con probabilidad  de alterar el valor de cada bit, transmite una palabra de código
de alterar el valor de cada bit, transmite una palabra de código
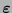 . Si
. Si
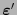 es la palabra recibida tras la transmisión, el error es
es la palabra recibida tras la transmisión, el error es
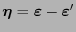 . El error quedará indetectado siempre que
. El error quedará indetectado siempre que
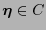 .
.
Para cada
![$i\in[\![1,2^m-1]\!]$](img415.png) , sea
, sea 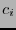 el número de palabras con peso de Hamming
el número de palabras con peso de Hamming  en el código
en el código  . Entonces, la probabilidad de que un error quede indetectado será
. Entonces, la probabilidad de que un error quede indetectado será
donde 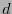 es el peso mínimo de
es el peso mínimo de  (si
(si  entonces
entonces 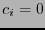 ).
).
Definición 4.9
El polinomio
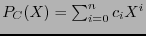 , donde
, donde 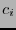 es el número de palabras con peso
es el número de palabras con peso  en
en  , se dice ser el enumerador de pesos del código
, se dice ser el enumerador de pesos del código  .
.
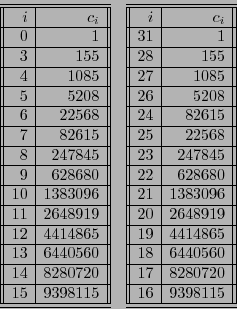
De acuerdo con lo anterior, se tiene
Por ejemplo, para los primeros códigos de Hamming se tiene:
 .
.- La dimensión del código es
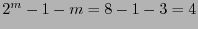 , por tanto el código posee
, por tanto el código posee 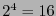 palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
El enumerador de pesos es pues
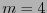 .
.- La dimensión del código es
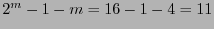 , por tanto el código posee
, por tanto el código posee 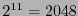 palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
El enumerador de pesos es pues
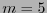 .
.- La dimensión del código es
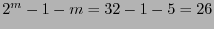 , por tanto el código posee
, por tanto el código posee
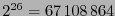 palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
palabras, que clasificadas según sus pesos de Hamming producen las siguientes cuentas:
Si se conoce el polinomio enumerador de pesos en un código-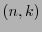
 se puede calcular procedimentalmente el polinomio enumerador de pesos de su dual
se puede calcular procedimentalmente el polinomio enumerador de pesos de su dual 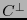 .
Denotemos por
.
Denotemos por 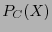 al enumerador de pesos de
al enumerador de pesos de  , según la definición 4.9. Definamos al polinomio de dos variables
, según la definición 4.9. Definamos al polinomio de dos variables
Teorema 4.1 (MacWilliams)
Para el código dual 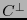 de
de  se tiene
o equivalentemente
se tiene
o equivalentemente
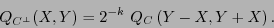 |
(8) |
Observamos primero
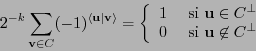 |
(9) |
En efecto, por un lado
 . Por otro, si
. Por otro, si
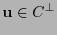 entonces
entonces
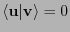 . En otro caso, existe
. En otro caso, existe
 tal que
tal que
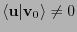 , es decir,
, es decir,
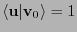 . Se puede ver que
. Se puede ver que
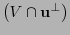 y
y
 forman una partición de
forman una partición de 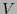 y ambas tienen una misma cardinalidad. De aquí se sigue (9).
y ambas tienen una misma cardinalidad. De aquí se sigue (9).
Observamos luego que, para cualquier código, se tiene
Pues bien, por un lado se tiene
Por otro lado,
Por tanto se cumple (8). 




Siguiente: Códigos lineales
Arriba: Códigos binarios
Anterior: Distancia de Hamming
Guillermo M. Luna
2010-05-09
![]() es
es
![]() , y el peso mínimo del código es
, y el peso mínimo del código es
![]() es
es
![]() , y el peso mínimo del código es
, y el peso mínimo del código es
![\begin{eqnarray*}
C &=& \left\lbrace \mbox{\boldmath$\varepsilon$}\in \mathbb{F}...
...epsilon_{\nu(i,j)}\right) \mbox{\rm mod }2 \right] \right\rbrace
\end{eqnarray*}](img353.png)
![]() es un código lineal, pues contiene al origen y es cerrado bajo la suma. Si un elemento
es un código lineal, pues contiene al origen y es cerrado bajo la suma. Si un elemento
![]() toma el valor
toma el valor ![]() , entonces debe aparecer un
, entonces debe aparecer un ![]() en otra posición en la misma columna y un
en otra posición en la misma columna y un ![]() también en otra posición en el mismo renglón, y debe haber un
también en otra posición en el mismo renglón, y debe haber un ![]() en la esquina opuesta a
en la esquina opuesta a ![]() . En consecuencia, el peso mínimo de
. En consecuencia, el peso mínimo de ![]() es
es ![]() y por tanto es capaz de detectar hasta 3 errores.
y por tanto es capaz de detectar hasta 3 errores.
![]() estará en el código si y sólo si se satisfacen las
estará en el código si y sólo si se satisfacen las ![]() ecuaciones
ecuaciones
![\begin{displaymath}\sum_{j=0}^{n-1}\varepsilon_{\nu(i,j)} = 0,\ i\in[\![0,m-1]\!...
...\ \sum_{i=0}^{m-1}\varepsilon_{\nu(i,j)}=0,\ j\in[\![0,n-1]\!].\end{displaymath}](img360.png)
![]() y por tanto ha de poseer una base. Cualquier palabra podrá ser escrita como una combinación lineal de los elementos en la base y por tanto las palabras en el código han de satisfacer un conjunto de ecuaciones lineales tal como en el caso de los códigos rectangulares.
y por tanto ha de poseer una base. Cualquier palabra podrá ser escrita como una combinación lineal de los elementos en la base y por tanto las palabras en el código han de satisfacer un conjunto de ecuaciones lineales tal como en el caso de los códigos rectangulares.
![]() es de dimensión
es de dimensión ![]() en
en
![]() , sea
, sea
![]() una base de
una base de ![]() . La matriz
. La matriz
![]() que posee como columnas a los vectores básicos, llamada generatriz de
que posee como columnas a los vectores básicos, llamada generatriz de ![]() , es de orden
, es de orden ![]() y determina un isomorfismo
y determina un isomorfismo
![]() ,
,
![]() . Existe entonces una matriz
. Existe entonces una matriz
![]() tal que
tal que
![]() . Así se ha de tener la equivalencia:
. Así se ha de tener la equivalencia:
![]() . La matriz
. La matriz ![]() se dice ser una revisora de paridad del código
se dice ser una revisora de paridad del código ![]() .
.
![]() el
el ![]() -ésimo vector de la base canónica,
-ésimo vector de la base canónica,
![]() . Denotemos también por
. Denotemos también por
![]() al vector que coincide con
al vector que coincide con ![]() salvo que en sus dos entradas
salvo que en sus dos entradas ![]() y
y ![]() posee el valor 1,
posee el valor 1,
![]() .
.
![]() queda determinada de manera única salvo el orden en el que se enumere a los elementos de
queda determinada de manera única salvo el orden en el que se enumere a los elementos de
![]() . Sea
. Sea
![]() la permutación que ordena a los índices de acuerdo con el peso de Hamming y en orden lexicográfico cuando haya coincidencia de pesos. Por ejemplo:
la permutación que ordena a los índices de acuerdo con el peso de Hamming y en orden lexicográfico cuando haya coincidencia de pesos. Por ejemplo:

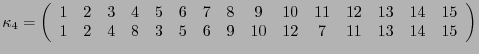
![$H_m=\left[\begin{array}{c} G_m \\ I_{2^m-1-m}\end{array}\right]\in\mathbb{F}_2^{\left(2^m-1\right)\times\left(2^m-1-m\right)}$](img402.png) . Entonces,
. Entonces,
![]() y por tanto las columnas de
y por tanto las columnas de ![]() forman una base del código de Hamming. La dimensión del código es el número de bits de información, a saber,
forman una base del código de Hamming. La dimensión del código es el número de bits de información, a saber, ![]() .
.
![]() se construye
se construye
![]() haciendo
haciendo
![]() para
para
![]() y, para
y, para
![]() , los valores
, los valores
![]() quedan determinados por la ec. (7).
quedan determinados por la ec. (7).
![]() , se revisa si éste está en el código. El vector
, se revisa si éste está en el código. El vector
![]() se dice ser el síndrome de
se dice ser el síndrome de
![]() . Si el síndrome fuese nulo no se hace ninguna corrección y se recupera
. Si el síndrome fuese nulo no se hace ninguna corrección y se recupera
![]() mediante los bits de información:
mediante los bits de información:
![]() , para
, para
![]() . En otro caso, deben existir
. En otro caso, deben existir
![]() en el código de Hamming y un índice
en el código de Hamming y un índice
![]() tales que
tales que
![]() . Por tanto, ha de tenerse
. Por tanto, ha de tenerse
![]() y
y
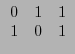 . De aquí se ve que la palabra
. De aquí se ve que la palabra
![]() , sea
, sea ![]() el número de palabras con peso de Hamming
el número de palabras con peso de Hamming ![]() en el código
en el código ![]() . Entonces, la probabilidad de que un error quede indetectado será
. Entonces, la probabilidad de que un error quede indetectado será