



Siguiente: Formas algebraicas
Arriba: Códigos de Reed-Muller
Anterior: Códigos de Reed-Muller
Definición 7.1 (Funciones booleanas)
Para cada
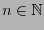 sea
sea
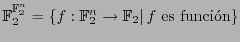 la colección de funciones booleanas.
la colección de funciones booleanas.
Naturalmente,
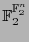 posee una estructura de álgebra booleana con
posee una estructura de álgebra booleana con 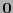 como elemento mínimo y
como elemento mínimo y 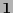 como elemento máximo. También, visto como un espacio vectorial sobre su campo primo
como elemento máximo. También, visto como un espacio vectorial sobre su campo primo 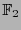 , la colección
, la colección
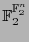 posee una estructura de espacio vectorial de dimensión
posee una estructura de espacio vectorial de dimensión 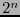 . Una base del espacio está dada por las funciones
. Una base del espacio está dada por las funciones
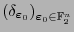 donde
donde
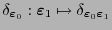 y esta última es la delta de Kroenecker.
y esta última es la delta de Kroenecker.
Observación 7.1
Las siguientas son identificaciones naturales entre respectivos conjuntos:
- La correspondencia
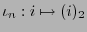 , que a cada entero le asocia su representación en base
, que a cada entero le asocia su representación en base 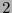 de longitud
de longitud  , identifica a
, identifica a
![$[\![0,2^n-1]\!]$](img688.png) con
con
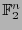 .
.
- La correspondencia
![$I_n:f\mapsto \left[f(\iota_n(i))\right]_{i\in[\![0,2^n-1]\!]} $](img689.png) , que a cada función booleana le asocia la cadena de sus valores de acuerdo con el orden de
, que a cada función booleana le asocia la cadena de sus valores de acuerdo con el orden de
![$[\![0,2^n-1]\!]$](img688.png) , identifica a
, identifica a
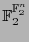 con
con
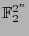 . Mediante tal identificación se dice que toda función booleana es una palabra-
. Mediante tal identificación se dice que toda función booleana es una palabra-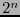 .
.
Las funciones proyecciones
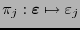 ,
,
![$j\in[\![0,n-1]\!]$](img692.png) , son funciones booleanas, y al formar un conjunto de
, son funciones booleanas, y al formar un conjunto de  funciones linealmente independientes, ellas mismas generan un espacio vectorial
funciones linealmente independientes, ellas mismas generan un espacio vectorial
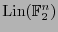 en
en
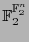 , llamado de las funciones lineales, isomorfo a
, llamado de las funciones lineales, isomorfo a
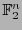 . De hecho, para cada
. De hecho, para cada
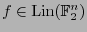 existe un único
existe un único
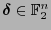 tal que
tal que
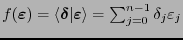 , para toda
, para toda
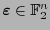 . Escribiremos
. Escribiremos
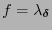 .
.
El complemento de una función booleana
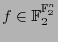 es
es
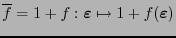 .
.
Los complementos de las funciones lineales son las funciones afines:
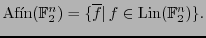
Recordamos que el producto en 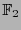 es idempotente,
es idempotente, 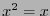 , y la suma es de orden 2:
, y la suma es de orden 2: 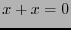 .
.




Siguiente: Formas algebraicas
Arriba: Códigos de Reed-Muller
Anterior: Códigos de Reed-Muller
Guillermo M. Luna
2010-05-09
![]() ,
,
![]() , son funciones booleanas, y al formar un conjunto de
, son funciones booleanas, y al formar un conjunto de ![]() funciones linealmente independientes, ellas mismas generan un espacio vectorial
funciones linealmente independientes, ellas mismas generan un espacio vectorial
![]() en
en
![]() , llamado de las funciones lineales, isomorfo a
, llamado de las funciones lineales, isomorfo a
![]() . De hecho, para cada
. De hecho, para cada
![]() existe un único
existe un único
![]() tal que
tal que
![]() , para toda
, para toda
![]() . Escribiremos
. Escribiremos
![]() .
.
![]() es
es
![]() .
.
![]()
![]() es idempotente,
es idempotente, ![]() , y la suma es de orden 2:
, y la suma es de orden 2: ![]() .
.