



Siguiente: Códigos de Reed-Muller
Arriba: Códigos de Reed-Muller
Anterior: Funciones booleanas
Sean
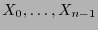
 símbolos de variables. Estas son pues entes sintácticos. A cada variable
símbolos de variables. Estas son pues entes sintácticos. A cada variable 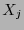 se le asocia con la proyección
se le asocia con la proyección 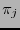 . Así la connotación de la variable
. Así la connotación de la variable 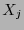 es el valor de la
es el valor de la 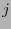 -ésima entrada en cada punto de
-ésima entrada en cada punto de
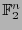 . Los monomios son productos de variables (distintas a pares) y los polinomios son combinaciones lineales de monomios. El grado de un monomio es el número de variables, distintas a pares, que aparecen en él como factores, y el grado de un polinomio es el mayor de los grados de los monomios que aparecen en él como sumandos. Un polinomio
. Los monomios son productos de variables (distintas a pares) y los polinomios son combinaciones lineales de monomios. El grado de un monomio es el número de variables, distintas a pares, que aparecen en él como factores, y el grado de un polinomio es el mayor de los grados de los monomios que aparecen en él como sumandos. Un polinomio
![$P(X_0,\ldots,X_{n-1})\in \mathbb{F}_2[X_0,\ldots,X_{n-1}]$](img708.png) define la función
define la función
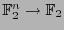 ,
,
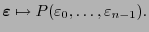
Definición 7.2
Para cada función booleana
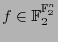 , su soporte es
, su soporte es
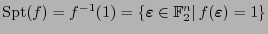 y su parte nula es
y su parte nula es
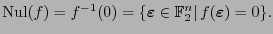 Así,
Así,
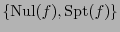 es una partición de
es una partición de
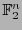 .
.
Definición 7.3
Las siguientes nociones son convencionales:
- Para cada variable
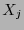 , se hace
, se hace 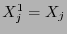 y
y 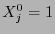 .
.
- Para cada
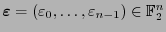 su monomio característico es
su monomio característico es
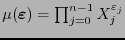 .
.
Observación 7.2
Las siguientes aseveraciones se cumplen para cada
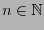 :
:
- Toda función booleana es equivalente a un polinomio. O si se quiere, toda palabra-
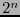 es equivalente a un polinomio.
es equivalente a un polinomio.
- Toda función es lineal o afín cuando y sólo cuando sea de grado a lo sumo
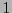 .
.
- El máximo grado posible es
 .
.
En efecto, puede verse que si
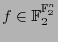 entonces ella coincide con la función
entonces ella coincide con la función
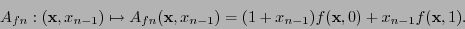 |
(14) |
Al representar a las funciones
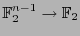 ,
,
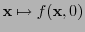 ,
,
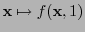 también como polinomios, de (14) se encuentra el polinomio equivalente a
también como polinomios, de (14) se encuentra el polinomio equivalente a 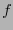 .
. 
Definición 7.4
El polinomio equivalente a
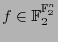 se dice ser la forma normal algebraica
se dice ser la forma normal algebraica
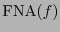 de
de 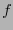 .
.
Una manera alternativa de calcular
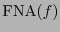 es la siguiente: Inicialmente hágase
es la siguiente: Inicialmente hágase
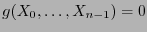 , y luego, para cada
, y luego, para cada
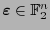 , si acaso
, si acaso
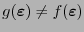 actualícese
actualícese
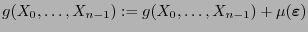 donde
donde
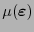 es el monomio característico de
es el monomio característico de
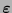 (véase la definición 7.3).
(véase la definición 7.3). 
Ahora bien, al ser 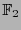 un campo, se tiene, por el Teorema Fundamental del Algebra, que cualquier polinomio en
un campo, se tiene, por el Teorema Fundamental del Algebra, que cualquier polinomio en
![$\mathbb{F}_2[X]$](img554.png) que sea no-nulo a lo más posee un número de raíces igual a su grado. De aquí se sigue:
que sea no-nulo a lo más posee un número de raíces igual a su grado. De aquí se sigue:
Observación 7.3
La colección
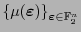 es linealmente independiente y por tanto es una base de
es linealmente independiente y por tanto es una base de
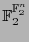 sobre
sobre 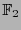 .
.
Observamos también que si
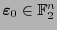 tiene un peso de Hamming
tiene un peso de Hamming
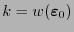 y es precisamente en los índices
y es precisamente en los índices
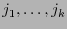 que
que
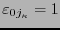 entonces para cualquier
entonces para cualquier
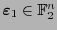 se tiene
se tiene
Es decir
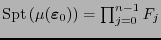 donde
donde 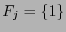 si
si
![$\exists\kappa\in[\![1,k]\!]$](img737.png) :
: 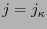 , o
, o 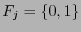 en otro caso.
en otro caso.
Observación 7.4
El soporte de cada monomio
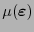 es una variedad lineal de dimensión
es una variedad lineal de dimensión
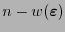 en
en
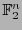 . Posee, por tanto,
. Posee, por tanto,
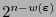 elementos.
elementos.




Siguiente: Códigos de Reed-Muller
Arriba: Códigos de Reed-Muller
Anterior: Funciones booleanas
Guillermo M. Luna
2010-05-09
![]() es la siguiente: Inicialmente hágase
es la siguiente: Inicialmente hágase
![]() , y luego, para cada
, y luego, para cada
![]() , si acaso
, si acaso
![]() actualícese
actualícese
![]() donde
donde
![]() es el monomio característico de
es el monomio característico de
![]() (véase la definición 7.3).
(véase la definición 7.3). ![]()
![]() un campo, se tiene, por el Teorema Fundamental del Algebra, que cualquier polinomio en
un campo, se tiene, por el Teorema Fundamental del Algebra, que cualquier polinomio en
![]() que sea no-nulo a lo más posee un número de raíces igual a su grado. De aquí se sigue:
que sea no-nulo a lo más posee un número de raíces igual a su grado. De aquí se sigue:
![]() tiene un peso de Hamming
tiene un peso de Hamming
![]() y es precisamente en los índices
y es precisamente en los índices
![]() que
que
![]() entonces para cualquier
entonces para cualquier
![]() se tiene
se tiene