



Siguiente: Codificación y decodificación
Arriba: Códigos cíclicos
Anterior: Códigos cíclicos
Definición 8.1
Sea 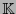 un campo finito. En el espacio
un campo finito. En el espacio 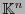 , la transformación lineal que sobre la base canónica actúa como
, la transformación lineal que sobre la base canónica actúa como
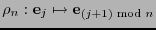 se dice ser la rotación de componentes.
Un código lineal-
se dice ser la rotación de componentes.
Un código lineal-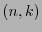
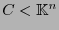 es cíclico si
es cíclico si
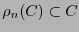 .
.
Sea ![$\mathbb{K}[X]$](img851.png) el anillo de polinomios sobre
el anillo de polinomios sobre 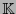 y sea
y sea
![$\iota_n: \mathbb{K}^n\to\mathbb{K}[X]$](img852.png) ,
,
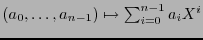 la transformación que a cada vector de
la transformación que a cada vector de  coeficientes lo convierte en el polinomio correspondiente.
coeficientes lo convierte en el polinomio correspondiente. 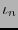 es, naturalmente, un monomorfismo lineal de espacios vectoriales sobre
es, naturalmente, un monomorfismo lineal de espacios vectoriales sobre 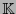 . Consideremos el polinomio
. Consideremos el polinomio 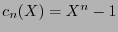 y al cociente
y al cociente
![$\mathbb{K}[X]/(c_n(X)) = \mathbb{K}[X]/(X^n-1)$](img856.png) el cual, visto como un espacio vectorial de dimensión
el cual, visto como un espacio vectorial de dimensión  , hace que
, hace que
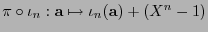 sea un isomorfismo lineal que aplica la base canónica de
sea un isomorfismo lineal que aplica la base canónica de 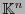 sobre la base polinomial
sobre la base polinomial
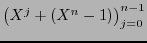 , donde
, donde
![$\pi:\mathbb{K}[X]\to\mathbb{K}[X]/(X^n-1)$](img859.png) es la proyección canónica
es la proyección canónica
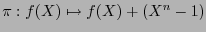 . Se tiene el diagrama:
. Se tiene el diagrama:
![\begin{displaymath}
\xymatrix{
\mathbb{K}^n\ar[dr]_{\pi_n\circ\iota_n} \ar[r]^{\...
... & \mathbb{K}[X] \ar[d]^{\pi_n} \\
& \mathbb{K}[X]/(X^n-1)
}
\end{displaymath}](img861.png) |
(19) |
Si
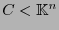 es un código cíclico entonces vale la implicación:
es un código cíclico entonces vale la implicación:
por tanto, la imagen
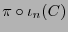 es un ideal en el anillo
es un ideal en el anillo
![$\mathbb{K}[X]/(X^n-1)$](img864.png) .
.
Como ![$\mathbb{K}[X]$](img851.png) es un anillo de ideales principales, necesariamente existe un polinomio
es un anillo de ideales principales, necesariamente existe un polinomio
![$g(X)\in\mathbb{K}[X]$](img865.png) tal que
tal que
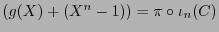 . Un tal polinomio con grado mínimo se dice ser generador del código
. Un tal polinomio con grado mínimo se dice ser generador del código  . De hecho el grado mínimo ha de ser
. De hecho el grado mínimo ha de ser 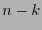 y en
y en ![$\mathbb{K}[X]$](img851.png) se ha de tener
se ha de tener 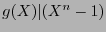 .
.
Recíprocamente, si
![$g(X)\in\mathbb{K}[X]$](img865.png) es tal que
es tal que 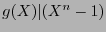 , el ideal generado por él, reducido módulo
, el ideal generado por él, reducido módulo 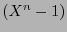 , consta de polinomios cuyos vectores de coeficientes forman un código cíclico
, consta de polinomios cuyos vectores de coeficientes forman un código cíclico  .
.
Observación 8.1
Así para cada  por cada divisor del polinomio
por cada divisor del polinomio 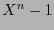 en
en ![$\mathbb{K}[X]$](img851.png) se tendrá un código cíclico.
se tendrá un código cíclico.
Hagamos aquí una breve disgresión sobre divisores del polinomio 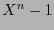 en campos finitos
en campos finitos
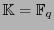 , donde
, donde 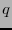 es la potencia de un primo. El orden de un polinomio no-nulo
es la potencia de un primo. El orden de un polinomio no-nulo
![$p(X)\in\mathbb{F}_{q}[X]$](img871.png) es el mínimo
es el mínimo  tal que
tal que 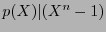 en
en
![$\mathbb{F}_{q}[X]$](img873.png) . Un polinomio
. Un polinomio
![$p(X)\in\mathbb{F}_{q}[X]$](img871.png) de grado
de grado
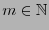 es primitivo si es el polinomio mínimo de un elemento primitivo, es decir, de un generador del grupo multiplicativo
es primitivo si es el polinomio mínimo de un elemento primitivo, es decir, de un generador del grupo multiplicativo
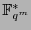 . Pues bien, se tiene que un polinomio de grado
. Pues bien, se tiene que un polinomio de grado 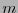 es primitivo cuando y sólo cuando su orden es
es primitivo cuando y sólo cuando su orden es 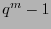 . Además, para cada
. Además, para cada 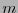 el número de polinomios primitivos de grado
el número de polinomios primitivos de grado 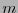 en
en
![$\mathbb{F}_{q}[X]$](img873.png) es
es 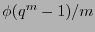 donde
donde 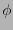 es la función tociente de Euler.
es la función tociente de Euler.
Así para un polinomio primitivo
![$g(X)\in\mathbb{F}_{2}[X]$](img879.png) de grado
de grado 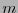 , de acuerdo con la observación 8.1, el tamaño de bloque para que
, de acuerdo con la observación 8.1, el tamaño de bloque para que 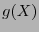 sea el generador de un código cíclico debe ser
sea el generador de un código cíclico debe ser 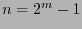 .
.
Sigamos con nuestra exposición. Si el polinomio generador de un código cíclico es
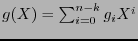 entonces
entonces
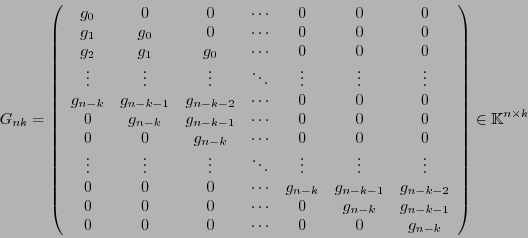 |
(20) |
es una generatriz del código  . El polinomio generador
. El polinomio generador 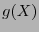 , que es único si se le supone mónico, es decir con coeficiente principal 1, determina pues por completo al código cíclico
, que es único si se le supone mónico, es decir con coeficiente principal 1, determina pues por completo al código cíclico  . Es convencional identificar a cada palabra de código
. Es convencional identificar a cada palabra de código 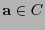 tanto con el polinomio
tanto con el polinomio
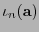 como con la clase
como con la clase
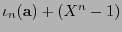 de ese polinomio y por tanto en el contexto de códigos cíclicos se dice que las palabras de código son polinomios.
de ese polinomio y por tanto en el contexto de códigos cíclicos se dice que las palabras de código son polinomios.
Este es un subespacio lineal y una matriz revisora de paridad es 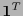 :
:
Por tanto 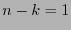 y consecuentemente
y consecuentemente  posee
posee 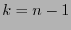 bits de información.
bits de información.
Claramente  es cíclico. Como la palabra
es cíclico. Como la palabra 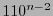 está en
está en  , el polinomio generador ha de ser
, el polinomio generador ha de ser 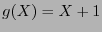 el cual evidentemente divide a
el cual evidentemente divide a
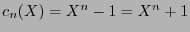 en
en
![$\mathbb{F}_2[X]$](img554.png) . Algunos ejemplos de generatrices son
. Algunos ejemplos de generatrices son
Así el código de palabras con peso par en
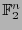 puede representarse de manera precisa con el solo polinomio
puede representarse de manera precisa con el solo polinomio 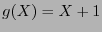 .
. 
Sea
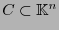 un código cíclico y sea
un código cíclico y sea
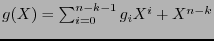 su polinomio generador. Como
su polinomio generador. Como 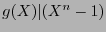 , el cociente
, el cociente
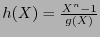 es un polinomio, de grado
es un polinomio, de grado 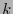 . Escribamos
. Escribamos
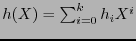 . Entonces,
. Entonces,
por lo cual en el campo 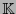 se ha de tener
se ha de tener
![\begin{displaymath}
g_{0} h_0 = 1\ \ \&\ \ \left[\ell\in[\![1,n-1]\!]\ \Rightarr...
...\ell,k\}} g_i h_{\ell-i} = 0\right]\ \ \&\ \ g_{n-k} h_k = 1.
\end{displaymath}](img899.png) |
(21) |
Al considerar un polinomio 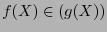 , necesariamente
, necesariamente
para algún
![$e(X)\in\mathbb{K}[X]$](img902.png) , o sea
, o sea
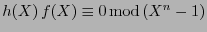 .
Es debido a esto último que el polinomio
.
Es debido a esto último que el polinomio 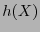 se dice ser el polinomio revisor de paridad del código cíclico
se dice ser el polinomio revisor de paridad del código cíclico  . De hecho la matriz
. De hecho la matriz
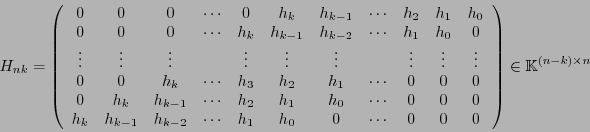 |
(22) |
es revisora de paridad del código  , pues por las relaciones (21) se ve que
, pues por las relaciones (21) se ve que
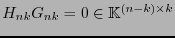 , es decir cada rengón de
, es decir cada rengón de 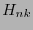 es ortogonal a todas las columnas de
es ortogonal a todas las columnas de 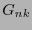 . Es importante remarcar que en la ec. (20) los índices son crecientes en cada columna, en tanto que en la ec. (22) son decrecientes en cada renglón. Se tiene pues:
. Es importante remarcar que en la ec. (20) los índices son crecientes en cada columna, en tanto que en la ec. (22) son decrecientes en cada renglón. Se tiene pues:
y en consecuencia
![\begin{displaymath}
\forall{\bf u},{\bf v}\in \mathbb{K}^n:\ \left[{\bf u}-{\bf v}\in C\ \Longrightarrow\ H_{nk}{\bf u} = H_{nk}{\bf v}\right] .
\end{displaymath}](img910.png) |
(23) |
Hay pues 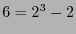 códigos cíclicos binarios de longitud
códigos cíclicos binarios de longitud 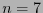 . En particular, para el polinomio
. En particular, para el polinomio
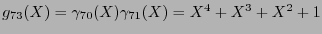 se tiene
se tiene
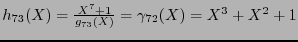 y las matrices generatriz y revisora de paridad siguientes:
y las matrices generatriz y revisora de paridad siguientes:
La función de codificación es pues
Este se dice ser el código ``símplex''. En los 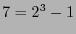 renglones de la matriz generatriz
renglones de la matriz generatriz 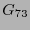 aparecen las representaciones en binario de los números en el intervalo
aparecen las representaciones en binario de los números en el intervalo
![$[\![1,2^3-1]\!]$](img926.png) , por tanto su código dual es uno de Hamming.
, por tanto su código dual es uno de Hamming. 
Hay pues 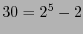 códigos cíclicos terciarios de longitud
códigos cíclicos terciarios de longitud 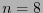 . En particular, para el polinomio
. En particular, para el polinomio
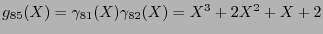 se tiene
se tiene
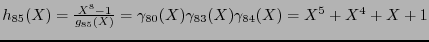 y las matrices generatriz y revisora de paridad siguientes:
y las matrices generatriz y revisora de paridad siguientes:





Siguiente: Codificación y decodificación
Arriba: Códigos cíclicos
Anterior: Códigos cíclicos
Guillermo M. Luna
2010-05-09
![]() el anillo de polinomios sobre
el anillo de polinomios sobre ![]() y sea
y sea
![]() ,
,
![]() la transformación que a cada vector de
la transformación que a cada vector de ![]() coeficientes lo convierte en el polinomio correspondiente.
coeficientes lo convierte en el polinomio correspondiente. ![]() es, naturalmente, un monomorfismo lineal de espacios vectoriales sobre
es, naturalmente, un monomorfismo lineal de espacios vectoriales sobre ![]() . Consideremos el polinomio
. Consideremos el polinomio ![]() y al cociente
y al cociente
![]() el cual, visto como un espacio vectorial de dimensión
el cual, visto como un espacio vectorial de dimensión ![]() , hace que
, hace que
![]() sea un isomorfismo lineal que aplica la base canónica de
sea un isomorfismo lineal que aplica la base canónica de ![]() sobre la base polinomial
sobre la base polinomial
![]() , donde
, donde
![]() es la proyección canónica
es la proyección canónica
![]() . Se tiene el diagrama:
. Se tiene el diagrama:
![]() es un anillo de ideales principales, necesariamente existe un polinomio
es un anillo de ideales principales, necesariamente existe un polinomio
![]() tal que
tal que
![]() . Un tal polinomio con grado mínimo se dice ser generador del código
. Un tal polinomio con grado mínimo se dice ser generador del código ![]() . De hecho el grado mínimo ha de ser
. De hecho el grado mínimo ha de ser ![]() y en
y en ![]() se ha de tener
se ha de tener ![]() .
.
![]() es tal que
es tal que ![]() , el ideal generado por él, reducido módulo
, el ideal generado por él, reducido módulo ![]() , consta de polinomios cuyos vectores de coeficientes forman un código cíclico
, consta de polinomios cuyos vectores de coeficientes forman un código cíclico ![]() .
.
![]() en campos finitos
en campos finitos
![]() , donde
, donde ![]() es la potencia de un primo. El orden de un polinomio no-nulo
es la potencia de un primo. El orden de un polinomio no-nulo
![]() es el mínimo
es el mínimo ![]() tal que
tal que ![]() en
en
![]() . Un polinomio
. Un polinomio
![]() de grado
de grado
![]() es primitivo si es el polinomio mínimo de un elemento primitivo, es decir, de un generador del grupo multiplicativo
es primitivo si es el polinomio mínimo de un elemento primitivo, es decir, de un generador del grupo multiplicativo
![]() . Pues bien, se tiene que un polinomio de grado
. Pues bien, se tiene que un polinomio de grado ![]() es primitivo cuando y sólo cuando su orden es
es primitivo cuando y sólo cuando su orden es ![]() . Además, para cada
. Además, para cada ![]() el número de polinomios primitivos de grado
el número de polinomios primitivos de grado ![]() en
en
![]() es
es ![]() donde
donde ![]() es la función tociente de Euler.
es la función tociente de Euler.
![]() de grado
de grado ![]() , de acuerdo con la observación 8.1, el tamaño de bloque para que
, de acuerdo con la observación 8.1, el tamaño de bloque para que ![]() sea el generador de un código cíclico debe ser
sea el generador de un código cíclico debe ser ![]() .
.
![]() entonces
entonces
![]() es cíclico. Como la palabra
es cíclico. Como la palabra ![]() está en
está en ![]() , el polinomio generador ha de ser
, el polinomio generador ha de ser ![]() el cual evidentemente divide a
el cual evidentemente divide a
![]() en
en
![]() . Algunos ejemplos de generatrices son
. Algunos ejemplos de generatrices son
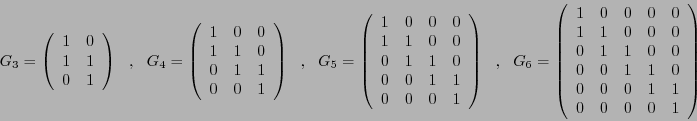
![]() un código cíclico y sea
un código cíclico y sea
![]() su polinomio generador. Como
su polinomio generador. Como ![]() , el cociente
, el cociente
![]() es un polinomio, de grado
es un polinomio, de grado ![]() . Escribamos
. Escribamos
![]() . Entonces,
. Entonces,
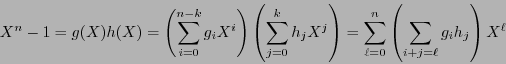
![\begin{displaymath}G_{73} = \left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\ ...
...0 & 1 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 & 0 & 0
\end{array}\right].\end{displaymath}](img922.png)
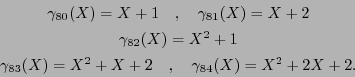
![\begin{displaymath}G_{85} = \left[\begin{array}{ccccc}
2 & 0 & 0 & 0 & 0 \\
1 &...
... & 0 \\
1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 %\\
\end{array}\right].\end{displaymath}](img940.png)