



Siguiente: Códigos de Golay
Arriba: Códigos cíclicos
Anterior: Polinomios generadores y revisores
Sea
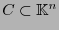 un código-
un código-![$[n,k]$](img326.png) cíclico, sea
cíclico, sea
![$g(X)\in\mathbb{K}[X]$](img865.png) su polinomio generador y sea
su polinomio generador y sea 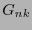 su matriz generatriz. Naturalmente, dada una palabra
su matriz generatriz. Naturalmente, dada una palabra
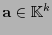 , ella ha de quedar codificada por la palabra
, ella ha de quedar codificada por la palabra
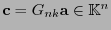 . Ya que la
. Ya que la 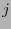 -ésima columna
-ésima columna 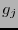 de la matriz generatriz
de la matriz generatriz 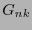 corresponde bajo la función
corresponde bajo la función 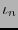 al polinomio
al polinomio 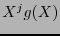 , se tiene
, se tiene
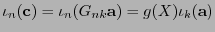 . En otras palabras, la manera de codificar a cada palabra es viéndola como un polinomio y multiplicando por éste al polinomio generador. Esta codificación mediante códigos cíclicos se dice ser no-sistemática.
. En otras palabras, la manera de codificar a cada palabra es viéndola como un polinomio y multiplicando por éste al polinomio generador. Esta codificación mediante códigos cíclicos se dice ser no-sistemática.
Definición 8.2
Sea
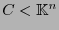 un código cíclico con polinomio generador
un código cíclico con polinomio generador 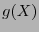 . Para cada
. Para cada
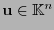 , sea
, sea
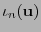 el polinomio con vector de coeficientes
el polinomio con vector de coeficientes 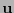 . El síndrome polinomial de
. El síndrome polinomial de 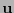 es el polinomio
es el polinomio
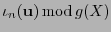 (o si se quiere, su vector de coeficientes).
(o si se quiere, su vector de coeficientes).
Esta definición concuerda con la 5.5. En efecto, para cada
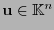 , al escribir
, al escribir
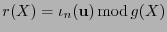 , entonces
, entonces
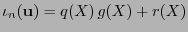 , con
, con
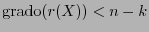 , para algún polinomio
, para algún polinomio 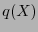 . Así, sea
. Así, sea
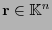 tal que
tal que
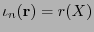 (como
(como
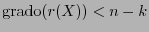 , las últimas
, las últimas 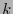 entradas de
entradas de 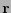 son 0). Por la relación (23),
son 0). Por la relación (23),
![\begin{displaymath}
H_{nk}{\bf u} = H_{nk}{\bf r} = \left[\, H_{nk}^{(n-k)}\ \ H...
... r}^{(k)}
\end{array}\right] = H_{nk}^{(n-k)}{\bf r}^{(n-k)},
\end{displaymath}](img957.png) |
(24) |
donde
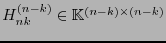 es la matriz formada por las primeras
es la matriz formada por las primeras 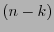 columnas de
columnas de 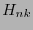 ,
,
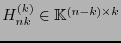 es la matriz formada por las últimas
es la matriz formada por las últimas 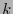 columnas de
columnas de 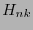 ,
,
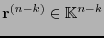 consta de las primeras
consta de las primeras 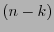 entradas de
entradas de 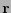 y
y
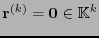 consta de las últimas
consta de las últimas 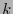 entradas de
entradas de 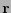 . El síndrome de
. El síndrome de 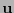 , en el sentido de la definición 5.5, es
, en el sentido de la definición 5.5, es 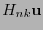 y, según la relación (24), éste es
y, según la relación (24), éste es
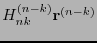 . Ya que
. Ya que
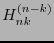 posee una forma triangular su determinante es
posee una forma triangular su determinante es
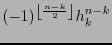 y es, por tanto, una matriz no singular. Esta determina un automorfismo lineal en
y es, por tanto, una matriz no singular. Esta determina un automorfismo lineal en
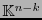 y la correspondencia entre los síndromes de la definición 5.5 y los de la 8.2.
y la correspondencia entre los síndromes de la definición 5.5 y los de la 8.2.
- Procedimiento de decodificación.
- Supóngase que al transmitir una palabra
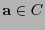 se recibiera la palabra
se recibiera la palabra
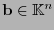 . El error cometido sería pues
. El error cometido sería pues
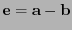 . Vistas las palabras como polinomios, al calcular el síndrome polinomial
. Vistas las palabras como polinomios, al calcular el síndrome polinomial
![$r(X)\in\mathbb{K}[X]$](img970.png) de
de 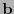 se tendrá que existe un polinomio
se tendrá que existe un polinomio
![$q(X)\in\mathbb{K}[X]$](img972.png) tal que
tal que
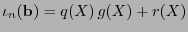 . Si la distancia mínima del código
. Si la distancia mínima del código  fuese
fuese 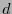 entonces habría que localizar una palabra
entonces habría que localizar una palabra 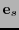 de peso de Hamming a lo sumo
de peso de Hamming a lo sumo
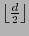 tal que
tal que
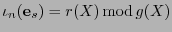 . Entonces necesariamente
. Entonces necesariamente
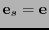 y en tal caso se corrige
y en tal caso se corrige 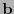 cambiándolo por
cambiándolo por
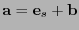 .
. 
El problema de cálculo de distancias mínimos de códigos cíclicos se ha tratado con diversos enfoques y el artículo de van Lint y Wilson [14] se ha convertido en una referencia clásica.
El proceso de decodificación descrito requiere pues calcular a los elementos con menor peso de Hamming en clases de congruencia módulo el polinomio generador.
Observamos que si
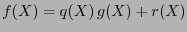 , con
, con
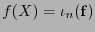 , al rotar
, al rotar 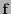 , valen:
, valen:

De esta manera, se puede calcular representantes principales para síndromes obtenidos de rotaciones de otros síndromes.
Por ejemplo, para el código-![$[7,3]$](img989.png) símplex tratado en el ejemplo 8.2, el polinomio generador es
símplex tratado en el ejemplo 8.2, el polinomio generador es
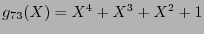 . Por tanto, módulo
. Por tanto, módulo 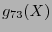 , se tiene
, se tiene
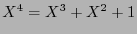 , y en consecuencia
, y en consecuencia
Así pues, en la base polinomial se tiene la correspondencia siguiente:
Dada una palabra 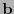 , se calcula su síndrome,
, se calcula su síndrome, 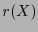 . Si éste aparece en el segundo renglón de la tabla anterior, entonces la correspondiente posición en el primero indicará cuál es el bit que hay que corregir. Si acaso el síndrome no apareciese, entonces, por tratarse de un código cíclico, la palabra puede rotarse y su síndrome multiplicarse por
. Si éste aparece en el segundo renglón de la tabla anterior, entonces la correspondiente posición en el primero indicará cuál es el bit que hay que corregir. Si acaso el síndrome no apareciese, entonces, por tratarse de un código cíclico, la palabra puede rotarse y su síndrome multiplicarse por 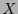 y reducirlo módulo
y reducirlo módulo 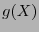 para volver a realizar la prueba.
para volver a realizar la prueba. 
Otra manera de codificación, llamada ésta sistemática, utilizando códigos cíclicos es la siguiente. Dada una palabra
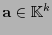 sea
sea
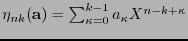 el polinomio de grado
el polinomio de grado 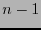 cuyos coeficientes ``más altos'' están dados por la palabra
cuyos coeficientes ``más altos'' están dados por la palabra 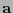 . Entonces ésta queda codificada por la palabra
. Entonces ésta queda codificada por la palabra
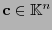 tal que
tal que
o puesto equivalentemente,
el cual polinomio, en efecto, está en el código cíclico  pues es un múltiplo del polinomio generador
pues es un múltiplo del polinomio generador 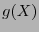 de
de  . La palabra
. La palabra
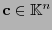 de código, se descompone naturalmente en dos tramos:
de código, se descompone naturalmente en dos tramos:
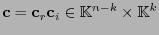 , tales que la parte ``alta''
, tales que la parte ``alta''
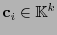 coincide con la palabra de información
coincide con la palabra de información 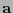 y la parte ``baja''
y la parte ``baja''
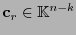 tiene fines de revisión de paridad.
tiene fines de revisión de paridad.
Ahora, si Alicia envíase una palabra de código
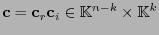 y Beto recibiese la palabra
y Beto recibiese la palabra
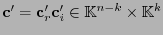 entonces Beto calcula el síndrome
entonces Beto calcula el síndrome
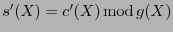 . Si acaso
. Si acaso 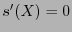 entonces Beto acepta a
entonces Beto acepta a 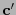 como
como 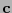 y no reconoce que hubiera habido errores. Si, en cambio,
y no reconoce que hubiera habido errores. Si, en cambio, 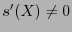 entonces reconoce que hubo errores y ha de proceder a corregirlos. Se ha de tener una tabla estándar de errores, de distancia de Hamming mínima, para algunos síndromes de manera que cuando se tenga un síndrome particular se lo localice en esa tabla para identificar el error del que proviene, y si no apareciese entonces se procede a rotar la palabra recibida y a multiplicar su síndrome por
entonces reconoce que hubo errores y ha de proceder a corregirlos. Se ha de tener una tabla estándar de errores, de distancia de Hamming mínima, para algunos síndromes de manera que cuando se tenga un síndrome particular se lo localice en esa tabla para identificar el error del que proviene, y si no apareciese entonces se procede a rotar la palabra recibida y a multiplicar su síndrome por 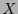 , reducirlo módulo
, reducirlo módulo 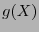 , y volver a realizar la prueba.
, y volver a realizar la prueba.




Siguiente: Códigos de Golay
Arriba: Códigos cíclicos
Anterior: Polinomios generadores y revisores
Guillermo M. Luna
2010-05-09
![]() un código-
un código-![]() cíclico, sea
cíclico, sea
![]() su polinomio generador y sea
su polinomio generador y sea ![]() su matriz generatriz. Naturalmente, dada una palabra
su matriz generatriz. Naturalmente, dada una palabra
![]() , ella ha de quedar codificada por la palabra
, ella ha de quedar codificada por la palabra
![]() . Ya que la
. Ya que la ![]() -ésima columna
-ésima columna ![]() de la matriz generatriz
de la matriz generatriz ![]() corresponde bajo la función
corresponde bajo la función ![]() al polinomio
al polinomio ![]() , se tiene
, se tiene
![]() . En otras palabras, la manera de codificar a cada palabra es viéndola como un polinomio y multiplicando por éste al polinomio generador. Esta codificación mediante códigos cíclicos se dice ser no-sistemática.
. En otras palabras, la manera de codificar a cada palabra es viéndola como un polinomio y multiplicando por éste al polinomio generador. Esta codificación mediante códigos cíclicos se dice ser no-sistemática.
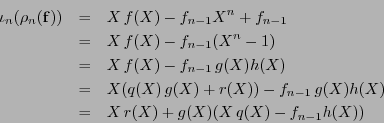
![]() símplex tratado en el ejemplo 8.2, el polinomio generador es
símplex tratado en el ejemplo 8.2, el polinomio generador es
![]() . Por tanto, módulo
. Por tanto, módulo ![]() , se tiene
, se tiene
![]() , y en consecuencia
, y en consecuencia
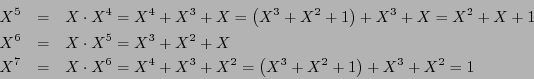
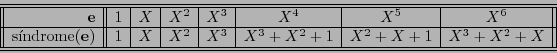
![]() sea
sea
![]() el polinomio de grado
el polinomio de grado ![]() cuyos coeficientes ``más altos'' están dados por la palabra
cuyos coeficientes ``más altos'' están dados por la palabra ![]() . Entonces ésta queda codificada por la palabra
. Entonces ésta queda codificada por la palabra
![]() tal que
tal que
![]() y Beto recibiese la palabra
y Beto recibiese la palabra
![]() entonces Beto calcula el síndrome
entonces Beto calcula el síndrome
![]() . Si acaso
. Si acaso ![]() entonces Beto acepta a
entonces Beto acepta a ![]() como
como ![]() y no reconoce que hubiera habido errores. Si, en cambio,
y no reconoce que hubiera habido errores. Si, en cambio, ![]() entonces reconoce que hubo errores y ha de proceder a corregirlos. Se ha de tener una tabla estándar de errores, de distancia de Hamming mínima, para algunos síndromes de manera que cuando se tenga un síndrome particular se lo localice en esa tabla para identificar el error del que proviene, y si no apareciese entonces se procede a rotar la palabra recibida y a multiplicar su síndrome por
entonces reconoce que hubo errores y ha de proceder a corregirlos. Se ha de tener una tabla estándar de errores, de distancia de Hamming mínima, para algunos síndromes de manera que cuando se tenga un síndrome particular se lo localice en esa tabla para identificar el error del que proviene, y si no apareciese entonces se procede a rotar la palabra recibida y a multiplicar su síndrome por ![]() , reducirlo módulo
, reducirlo módulo ![]() , y volver a realizar la prueba.
, y volver a realizar la prueba.