



Siguiente: Códigos de Reed-Solomon
Arriba: Códigos cíclicos
Anterior: Códigos de Golay
Sea
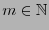 un entero positivo. En
un entero positivo. En
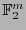 consideremos la relación de equivalencia:
consideremos la relación de equivalencia:
Es decir, las palabras
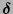 y
y
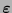 son equivalentes si coinciden salvo una rotación de sus símbolos. Una palabra
son equivalentes si coinciden salvo una rotación de sus símbolos. Una palabra
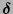 se dice poseer un patrón de error de ráfaga de longitud
se dice poseer un patrón de error de ráfaga de longitud  si para alguna palabra
si para alguna palabra
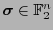 se cumple que
se cumple que
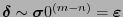 , es decir, si la parte no nula de la palabra es de longitud a lo sumo
, es decir, si la parte no nula de la palabra es de longitud a lo sumo  (acaso identificando sus extremos). Si para dos palabras
(acaso identificando sus extremos). Si para dos palabras
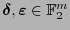 se tiene que el ``error'' entre ellas
se tiene que el ``error'' entre ellas
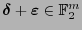 es un patrón de error de ráfaga de longitud
es un patrón de error de ráfaga de longitud  , entonces se dice que ellas difieren por una ráfaga de longitud
, entonces se dice que ellas difieren por una ráfaga de longitud  .
.
Proposición 8.2
Sea  un código-
un código-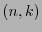 cíclico. Supongamos que al transmitir una palabra codificada
cíclico. Supongamos que al transmitir una palabra codificada
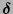 se han modificado
se han modificado 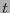 caracteres.
caracteres.
- Si el síndrome posee un peso de Hamming a lo sumo
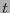 , entonces ha de coincidir con el patrón de error.
, entonces ha de coincidir con el patrón de error.
- Si se supone que los errores sólo pueden aparecer en
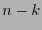 posiciones contiguas, entonces alguna rotación de
posiciones contiguas, entonces alguna rotación de
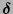 posee un síndrome con peso de Hamming a lo sumo
posee un síndrome con peso de Hamming a lo sumo 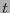 .
.
En efecto, se tiene
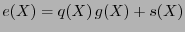 , donde
, donde 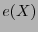 es el polinomio de error,
es el polinomio de error, 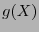 es un generador del código y
es un generador del código y 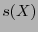 es el polinomio de índrome. Entonces,
es el polinomio de índrome. Entonces,
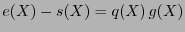 está en el código. Si el peso de Hamming de
está en el código. Si el peso de Hamming de 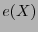 es a lo sumo
es a lo sumo 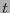 entonces
entonces 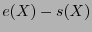 posee un peso de Hamming a lo sumo
posee un peso de Hamming a lo sumo 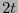 . Ya que
. Ya que  corrige a lo más
corrige a lo más 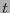 errores, su distancia mínima es
errores, su distancia mínima es 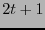 . Por tanto
. Por tanto 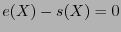 y
y 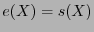 . La segunda aseveración se sigue de ésta inmediatamente.
. La segunda aseveración se sigue de ésta inmediatamente. 




Siguiente: Códigos de Reed-Solomon
Arriba: Códigos cíclicos
Anterior: Códigos de Golay
Guillermo M. Luna
2010-05-09
![]() un entero positivo. En
un entero positivo. En
![]() consideremos la relación de equivalencia:
consideremos la relación de equivalencia:
![]() , donde
, donde ![]() es el polinomio de error,
es el polinomio de error, ![]() es un generador del código y
es un generador del código y ![]() es el polinomio de índrome. Entonces,
es el polinomio de índrome. Entonces,
![]() está en el código. Si el peso de Hamming de
está en el código. Si el peso de Hamming de ![]() es a lo sumo
es a lo sumo ![]() entonces
entonces ![]() posee un peso de Hamming a lo sumo
posee un peso de Hamming a lo sumo ![]() . Ya que
. Ya que ![]() corrige a lo más
corrige a lo más ![]() errores, su distancia mínima es
errores, su distancia mínima es ![]() . Por tanto
. Por tanto ![]() y
y ![]() . La segunda aseveración se sigue de ésta inmediatamente.
. La segunda aseveración se sigue de ésta inmediatamente. ![]()