



Siguiente: Códigos de ráfagas
Arriba: Códigos cíclicos
Anterior: Codificación y decodificación
Por tanto todo código-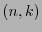
 perfecto para
perfecto para 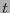 errores ha de corregir
errores ha de corregir 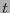 errores y en consecuencia su peso mínimo ha de ser
errores y en consecuencia su peso mínimo ha de ser 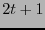 .
.
En efecto, 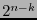 es el número de clases laterales módulo
es el número de clases laterales módulo  en tanto que
en tanto que
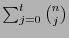 es el número de representantes principales de clases con pesos a lo sumo
es el número de representantes principales de clases con pesos a lo sumo 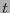 .
. 
A manera de recíproco, se tiene:
Observación 8.4
Si
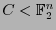 es un código-
es un código-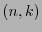 que corrige
que corrige 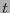 errores y
errores y
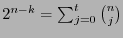 entonces es perfecto.
entonces es perfecto.
En la tabla 4 presentamos una lista de tercetas de enteros 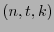 tales que se cumple (25).
tales que se cumple (25).
Recuadro 4:
Tercetas de enteros 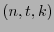 tales que
tales que
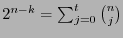 , con
, con 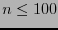 .
.
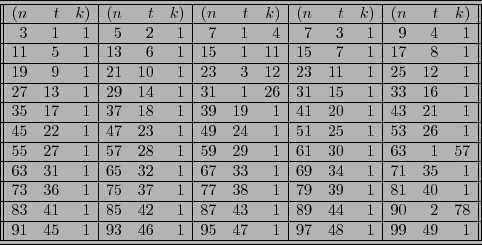 |
En la tercera columna, tercer rengón de ella aparece la terceta
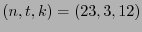 por lo cual ha de existir un código-
por lo cual ha de existir un código-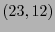
 perfecto para
perfecto para 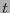 errores.
errores.
Proposición 8.1 (Golay, 1949)
El código cíclico de longitud 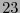 con polinomio generador
y por consiguiente con polinomio revisor de paridad
es perfecto para
con polinomio generador
y por consiguiente con polinomio revisor de paridad
es perfecto para 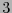 errores. Se le llama código de Golay.
errores. Se le llama código de Golay.




Siguiente: Códigos de ráfagas
Arriba: Códigos cíclicos
Anterior: Codificación y decodificación
Guillermo M. Luna
2010-05-09
![]() tales que se cumple (25).
tales que se cumple (25).