Siguiente: Códigos RS: Como códigos Arriba: Códigos de Reed-Solomon Anterior: Códigos de Reed-Solomon

Códigos RS: Como códigos de evaluación

Sea $q$ una potencia de un primo $p$ y $k\in\mathbb{N}$. Sean $a_0,\ldots,a_{n-1}\in\mathbb{F}_{q}$ $n$ puntos distintos. Se define $\Phi_0:\mathbb{F}_{q}^k\to\mathbb{F}_{q}[X]$ como ${\bf c}\mapsto \sum_{j=0}^{k-1} c_jX^j$, es decir como la función que a cada vector de $k$ entradas le asocia el polinomio cuyos coeficientes son esas entradas, y se define

$$\Phi_1:\mathbb{F}_{q}^k\to\mathbb{F}_{q}^n\ ,\ {\bf c}\mapsto... ...i_0({\bf c})(a_i)=\sum_{j=0}^{k-1} c_ja_i^j\right)_{i=0}^{n-1}.$$

El código de Reed-Solomon $\mbox{\rm RS}_e(q,n,k)$ es $\Phi_1(\mathbb{F}_{q}^k)$. Una matriz generatriz es pues

$$\left[a_i^j\right]_{(i,j)\in[\![0,n-1]\!]\times[\![0,k-1]\!]}\in\mathbb{F}_{q}^{n\times k}.$$

$\mbox{\rm RS}_e(q,n,k)$ es pues un código lineal y su distancia mínima es $n+1-k$ (si ${\bf c},{\bf d}\in\mathbb{F}_{q}^k$ son distintos, los polinomios que determinan, $\Phi_0({\bf c})$ y $\Phi_0({\bf d})$, pueden coincidir en a lo sumo $k-1$ puntos, por tanto han de discrepar en al menos $n-k+1$ puntos en $\{a_0,\ldots,a_{n-1}\}$).

Proposición 8.3   Dados una potencia de un primo $q$ y $k,n\in\mathbb{N}$ tales que $k\leq n\leq q$, existe un código-$(n,k,n-k+1)$ lineal sobre $\mathbb{F}_{q}$.

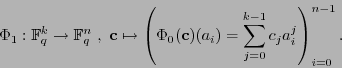
A saber, basta con dar $\mbox{\rm RS}_e(q,n,k)$. $\Box$

Para $q=2^8=256$, $n=q$ y $k=240$, $\mbox{\rm RS}_e(256,256,240)$ es un código-$(256,240,17)$ lineal que se utiliza en discos compactos.

Sea $a\in\mathbb{F}_{q}$ un elemento primitivo, es decir un generador de $\mathbb{F}_{q}^*$ y sea $n\in\mathbb{N}$ un entero que no sea múltiplo de la característica $p$ de $\mathbb{F}_{q}$. Entonces $q$ está en el grupo multiplicativo $\mathbb{Z}_n^*$. Sea $m=o_{\mathbb{Z}_n^*}(q)$ el orden de $q$ en $\mathbb{Z}_n^*$. Luego, $q^m=1\bmod n$. Sea $\rho=a^{\frac{q^m-1}{n}}$. Claramente $\rho^n=1$ en $\mathbb{F}_q$. Así pues la sucesión $\left(\rho^i\right)_{i=0}^{n-1}$ consta de las raíces $n$-ésimas de la unidad en $\mathbb{F}_{q}$. Al tomar como puntos de evaluación $a_i=\rho^i$, $i\in[\![0,n-1]\!]$, se tendrá que la matriz generatriz de $\mbox{\rm RS}_e(q,n,k)$ es $\left[\rho^{ij}\right]_{(i,j)\in[\![0,n-1]\!]\times[\![0,k-1]\!]}\in\mathbb{F}_{q}^{n\times k}.$

Siguiente: Códigos RS: Como códigos Arriba: Códigos de Reed-Solomon Anterior: Códigos de Reed-Solomon