



Siguiente: Decodificación de Reed-Solomon
Arriba: Códigos de Reed-Solomon
Anterior: Códigos RS: Como códigos
Si en el campo
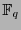 consideramos
consideramos 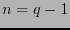 , entonces las raíces
, entonces las raíces  -ésimas de la unidad en
-ésimas de la unidad en
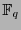 son todos sus elementos no-nulos, es decir, los elementos del grupo mutiplicativo, y el código de Reed-Solomon será cíclico. Veamos esto con detalle. Seguiremos aquí la presentación hecha en [4].
son todos sus elementos no-nulos, es decir, los elementos del grupo mutiplicativo, y el código de Reed-Solomon será cíclico. Veamos esto con detalle. Seguiremos aquí la presentación hecha en [4].
Sea
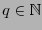 la potencia de un número primo
la potencia de un número primo  y sea
y sea
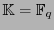 el campo de Galois de
el campo de Galois de 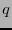 elementos, de característica
elementos, de característica  . Sea
. Sea
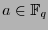 un elemento primitivo, vale decir, un generador del grupo cíclico multiplicativo
un elemento primitivo, vale decir, un generador del grupo cíclico multiplicativo
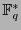 . Para
. Para  , sea
, sea 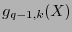 el polinomio
el polinomio
Como
![$\forall \kappa\in[\![1,q-1-k]\!]$](img1075.png) ,
,
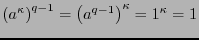 , se tiene
, se tiene
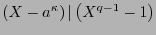 , y por tanto
, y por tanto
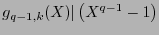 .
.
El código de Reed-Solomon
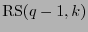 de longitud
de longitud 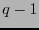 y dimensión
y dimensión 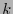 es el código cíclico generado por el polinomio
es el código cíclico generado por el polinomio 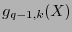 . Por tanto:
. Por tanto:
Observamos aquí que la última subcondición puede sustituirse por la que impone que 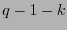 potencias consecutivas de
potencias consecutivas de  son raíces de
son raíces de 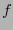 (esto porque el código es cíclico). Observamos también que si
(esto porque el código es cíclico). Observamos también que si  no fuese primitivo, entonces ha de generar un subgrupo de
no fuese primitivo, entonces ha de generar un subgrupo de
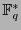 , por tanto el orden ha de ser un divisor de
, por tanto el orden ha de ser un divisor de 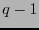 . Se tendría entonces un código de menor tamaño, pero también cíclico.
. Se tendría entonces un código de menor tamaño, pero también cíclico.
Al escribir a un elemento
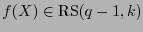 como
como
 , se tiene
, se tiene
![$\forall \kappa\in[\![1,q-1-k]\!]$](img1075.png)
donde
Por tanto una matriz revisora de paridad del código
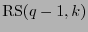 es:
es:
![\begin{displaymath}
\mbox{\rm RS}_{q-1,k}^{\perp} = \left[a^{\kappa\lambda}\righ...
... %\\
\end{array}\right]\in\mathbb{F}_q^{(q-1-k)\times(q-1)}.
\end{displaymath}](img1087.png) |
(26) |
Observación 8.5
Cualesquiera 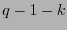 columnas de la matriz
columnas de la matriz
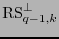 , dada por (26), son linealmente independientes en
, dada por (26), son linealmente independientes en
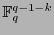 . En otras palabras, al tomar cualesquiera
. En otras palabras, al tomar cualesquiera 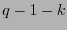 columnas de la matriz
columnas de la matriz
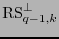 , la submatriz resultante es no-singular.
, la submatriz resultante es no-singular.
Observación 8.6
El código
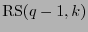 tiene distancia mínima
tiene distancia mínima 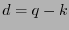 .
.
En efecto, por la observación anterior  . Por la desigualdad de Singleton
. Por la desigualdad de Singleton  .
. 
Dada una palabra
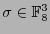 , digamos
, digamos
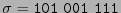 , ésta puede identificarse con el polinomio
, ésta puede identificarse con el polinomio
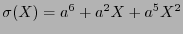 . Al codificarlo, se obtiene el polinomio
. Al codificarlo, se obtiene el polinomio
el cual polinomio representa a la 7-palabra
 Así pues, el código
Así pues, el código
 establece la correspondencia
establece la correspondencia
 .
. 




Siguiente: Decodificación de Reed-Solomon
Arriba: Códigos de Reed-Solomon
Anterior: Códigos RS: Como códigos
Guillermo M. Luna
2010-05-09
![]() consideramos
consideramos ![]() , entonces las raíces
, entonces las raíces ![]() -ésimas de la unidad en
-ésimas de la unidad en
![]() son todos sus elementos no-nulos, es decir, los elementos del grupo mutiplicativo, y el código de Reed-Solomon será cíclico. Veamos esto con detalle. Seguiremos aquí la presentación hecha en [4].
son todos sus elementos no-nulos, es decir, los elementos del grupo mutiplicativo, y el código de Reed-Solomon será cíclico. Veamos esto con detalle. Seguiremos aquí la presentación hecha en [4].
![]() la potencia de un número primo
la potencia de un número primo ![]() y sea
y sea
![]() el campo de Galois de
el campo de Galois de ![]() elementos, de característica
elementos, de característica ![]() . Sea
. Sea
![]() un elemento primitivo, vale decir, un generador del grupo cíclico multiplicativo
un elemento primitivo, vale decir, un generador del grupo cíclico multiplicativo
![]() . Para
. Para ![]() , sea
, sea ![]() el polinomio
el polinomio

![]() de longitud
de longitud ![]() y dimensión
y dimensión ![]() es el código cíclico generado por el polinomio
es el código cíclico generado por el polinomio ![]() . Por tanto:
. Por tanto:
![]() como
como
![]() , se tiene
, se tiene
![]()
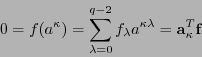
![\begin{displaymath}{\bf a}_{\kappa} = \left[\begin{array}{c}
1 \\ a^{\kappa} \\ ...
...n{array}{c}
f_0 \\ f_1 \\ \vdots \\ f_{q-2}
\end{array}\right].\end{displaymath}](img1086.png)
![]() . Por la desigualdad de Singleton
. Por la desigualdad de Singleton ![]() .
. ![]()
![]() , digamos
, digamos
![]() , ésta puede identificarse con el polinomio
, ésta puede identificarse con el polinomio
![]() . Al codificarlo, se obtiene el polinomio
. Al codificarlo, se obtiene el polinomio