1. Sea ![]() un elemento primitivo en un campo
un elemento primitivo en un campo ![]() . Demuestre las siguientes dos implicaciones:
. Demuestre las siguientes dos implicaciones:
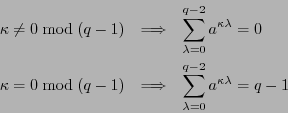
2. Sea
![]() un polinomio generador de un código cíclico-
un polinomio generador de un código cíclico-![]() . Calcule el polinomio de paridad
. Calcule el polinomio de paridad ![]() de
de ![]() .
.
3. Sea
![]() un polinomio de grado
un polinomio de grado
![]() que no sea un binomio, y sea
que no sea un binomio, y sea ![]() el entero mínimo tal que
el entero mínimo tal que ![]() divide a
divide a ![]() . Muestre que el código cíclico de longitud
. Muestre que el código cíclico de longitud ![]() generado por
generado por ![]() tiene peso mínimo al menos 3.
tiene peso mínimo al menos 3.
4. Sea ![]() un código cíclico-
un código cíclico-![]() binario. Muestre que si
binario. Muestre que si ![]() es impar y
es impar y ![]() no divide a
no divide a ![]() entonces el vector constante 1,
entonces el vector constante 1, ![]() , está en el código
, está en el código ![]() .
.
5. Sea
![]() un polinomio generador de un código cíclico-
un polinomio generador de un código cíclico-![]() . Calcule el síndrome del polinomio
. Calcule el síndrome del polinomio
![]() y decida si
y decida si ![]() está o no en el código.
está o no en el código.
6. Sea ![]() el código-
el código-![]() cíclico binario generado por el polinomio
cíclico binario generado por el polinomio ![]() , y suponga que se ha recibido el polinomio
, y suponga que se ha recibido el polinomio
![]() cuando se ha utilizado una codificación no-sistemática. Recupere el mensaje
cuando se ha utilizado una codificación no-sistemática. Recupere el mensaje ![]() que le dió origen.
que le dió origen.
7. Sea
![]() la matriz revisora de paridad del código de Hamming-
la matriz revisora de paridad del código de Hamming-
![]() , dado en la definición 4.7, y sea
, dado en la definición 4.7, y sea
![]() el código cuya generatriz es
el código cuya generatriz es ![]() .
.
8. Sea
![]() la matriz revisora de paridad del código de Hamming-
la matriz revisora de paridad del código de Hamming-
![]() , dado en la definición 4.7, y sea
, dado en la definición 4.7, y sea
![]() el código cuya generatriz es
el código cuya generatriz es ![]() .
.
9. Código CRC-16. Sea
![]() , el llamado polinomio CRC-16. Se tiene que, en
, el llamado polinomio CRC-16. Se tiene que, en
![]() :
:
10. Código CRC-CCITT. Sea
![]() , el llamado polinomio CRC-CCITT. Se tiene que, en
, el llamado polinomio CRC-CCITT. Se tiene que, en
![]() :
:
11. El código de Golay es un código-![]() perfecto de distancia mínima 7.
perfecto de distancia mínima 7.
12. Encuentre el polinomio generador de un código de BCH de longitud 31 que corrija errores dobles y el de otro que corrija errores triples.
13. Encuentre el polinomio generador de un código de Reed-Solomon con símbolos en
![]() que corrija errores dobles.
que corrija errores dobles.
14. ¿Cuántos códigos cíclicos de longitud ![]() hay sobre
hay sobre ![]() ?
?