Espacios proyectivos

Sea $\mathbb{K}$ un campo y sea $V$ un espacio vectorial sobre $\mathbb{K}$ . Sea L$(V)$ la clase de automorfismos lineales en $V$ , GL$(V)\subset$   L$(V)$ la de los invertibles, y SL$(V)\subset$   GL$(V)$ la de los que tienen determinante 1. Cuando el campo es el de los complejos, $\mathbb{K}=\mathbb{C}$ , U$(V)$ es el grupo de automorfismos lineales hermitianos, y SU$(V)\subset$   U$(V)$ el de aquellos con determinante 1.

En $V-\{{\bf0}\}$ se define la relación: $\left[{\bf x} \sim {\bf y} \Longleftrightarrow \exists a\in\mathbb{K}^*: {\bf y} = a{\bf x}\right].$ Se tiene entonces ${\bf x} \sim {\bf y}$ cuando y sólo cuando la matriz $[{\bf x} {\bf y}]$ es de rango a lo sumo 1. El espacio proyectivo es el cociente $\mathbb{P}(V) = (V-\{{\bf0}\})/\sim$ .

Cuando $V=\mathbb{K}^{n+1}$ , entonces $\mathbb{P}^n=\mathbb{P}(\mathbb{K}^{n+1})$ es el espacio proyectivo de dimensión $n$ sobre el campo $\mathbb{K}$ .

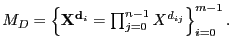Sea $D=\left(d_{ij}\right)_{(i,j)\in[\![0,m-1]\!]\times[\![0,n-1]\!]}\in\mathbb{Z}^{m\times n}$ una matriz de orden $m\times n$ con entradas en $\mathbb{Z}$ . Dada una colección ${\bf X}=\{X_0,\ldots,X_{n-1}\}$ de $n$ variables formales, la colección de monomios de Laurent determinada por $D$ es $M_D = \left\{{\bf X}^{{\bf d}_i} = \prod_{j=0}^{n-1}X^{d_{ij}}\right\}_{i=0}^{m-1}.$ El conjunto afín parametrizado por $D$ es $P_D = \left\{ \left({\bf x}^{{\bf d}_0},\ldots,{\bf x}^{{\bf d}_{m-1}}\right)\in\mathbb{K}^m\vert {\bf x}\in(\mathbb{K}^*)^n\right\}$ , pero, de hecho, debido a la homogeneidad de los polinomios de Laurent, el conjunto parametrizado puede considerarse como un subconjunto del espacio proyectivo de dimensión $m-1$ , $P_D\subset\mathbb{P}^{m-1}$ .

Un conjunto tórico algebraico es un conjunto $P\subset\mathbb{P}^{m-1}$ tal que existe una matriz $D\in\mathbb{Z}^{m\times n}$ para la cual $P=P_D$ .

Para cada $d\in\mathbb{N}$ sea $\mathbb{K}[{\bf X}]_d$ la colección de polinomios homogéneos de grado $d$ . Entonces $\oplus_{d=0}^{+\infty}\mathbb{K}[{\bf X}]_d$ es una graduación del anillo $\mathbb{K}[{\bf X}]$ .

Sea $I(P_D)\subset\mathbb{K}[{\bf X}]$ el ideal generado por los polinomios homogéneos que se anulan en $P_D$ , llamado ideal anulador de $P_D$ . Se verá algunas propiedades estructurales del ideal $I(P_D)$ .

Recordamos que en un anillo $R$ , para un ideal $I\subset R$ , su radical es rad$(I) = \{x\in R\vert \exists n\in\mathbb{Z}^+: x^n\in I\}$ , que en sí es un ideal, y el ideal $I$ es radical si $I=$rad$(I)$ .

Pues bien, puede verse que $I(P_D)$ es un ideal radical.