




Next: Variedades tóricas
Up: Curvas afines y proyectivas
Previous: Curvas afines y proyectivas
Contents
Index
Supongamos que
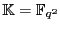 donde
donde 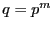 es una potencia de un primo. Sea
es una potencia de un primo. Sea
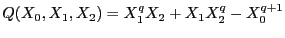 , entonces, como la característica del campo divide a
, entonces, como la característica del campo divide a 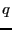 , se tiene
, se tiene
 ,
,
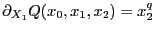 y
y
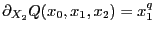 . En consecuencia la curva proyectiva
. En consecuencia la curva proyectiva
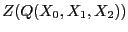 es suave.
es suave.
En lo que sigue, curva se referirá siempre a curva proyectiva suave.
Sea
![$ Q(X_0,X_1,X_2)\in\mathbb{K}[X_0,X_1,X_2]$](img479.png) un polinomio irreducible y sea
Q
un polinomio irreducible y sea
Q la curva que define. Sea
la curva que define. Sea
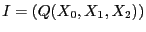 el ideal generado por
el ideal generado por
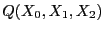 en el anillo
en el anillo
![$ \mathbb{K}[X_0,X_1,X_2]$](img502.png) , entonces
, entonces 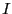 es primo y el cociente
es primo y el cociente
![$ \mathbb{K}[X_0,X_1,X_2]/I$](img503.png) es un dominio entero. Si
es un dominio entero. Si
![$ R(X_0,X_1,X_2)\in\mathbb{K}[X_0,X_1,X_2]$](img504.png) es un polinomio homogéneo de grado
es un polinomio homogéneo de grado 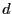 , se dice que el elemento
, se dice que el elemento
![$ R(X_0,X_1,X_2)+I\in\mathbb{K}[X_0,X_1,X_2]/I$](img505.png) es una forma de grado
es una forma de grado 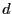 . La colección de formas racionales sobre la curva
Q
es
. La colección de formas racionales sobre la curva
Q
es
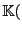
Q
![$\displaystyle ) = \left\{\frac{g}{h}\vert g,h\in\mathbb{K}[X_0,X_1,X_2]/I \mbox{ son formas del mismo grado y }h\not=0\right\}.$](img507.png)
Una forma racional
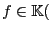 Q
Q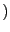 está definida en un punto
está definida en un punto
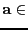 Q
de la curva si existen dos polinomios
Q
de la curva si existen dos polinomios
![$ A(X_0,X_1,X_2),B(X_0,X_1,X_2)\in\mathbb{K}[X_0,X_1,X_2]$](img511.png) tales que
tales que
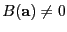 y
y
 .
Sea
.
Sea
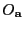 el anillo de funciones racionales definidas en
el anillo de funciones racionales definidas en  . Se tiene que
. Se tiene que
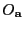 es un dominio entero y, de hecho, su campo de fracciones es precisamente
es un dominio entero y, de hecho, su campo de fracciones es precisamente
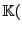 Q
Q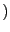 . Sea
. Sea
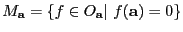 . Entonces
. Entonces
 es un ideal principal. Cualquier generador de él se dice ser un parámetro local en
es un ideal principal. Cualquier generador de él se dice ser un parámetro local en  .
.
Sea
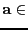 Q
y
Q
y
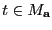 un parámetro local en
un parámetro local en  . Sea
. Sea
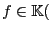 Q
Q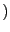 una función racional tal que
una función racional tal que 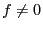 . Entonces existen
. Entonces existen
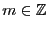 y
y
 tales que
tales que  . El entero
. El entero 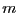 se dice ser la valuación de
se dice ser la valuación de 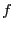 en
en  y se escribe
y se escribe
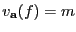 . Se tiene que
. Se tiene que
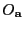 consiste de las funciones racionales con valuación no-negativa y
consiste de las funciones racionales con valuación no-negativa y
 de las racionales con valuación positiva.
de las racionales con valuación positiva.
Si
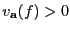 entonces
entonces  es un cero de multiplicidad
es un cero de multiplicidad
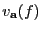 de
de 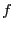 . Si
. Si
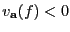 entonces
entonces  es un polo de multiplicidad
es un polo de multiplicidad
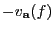 de
de 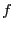 .
.
Teorema 2.4
Cualquier función racional tiene el mismo número de ceros que de polos (contados con multiplicidades).





Next: Variedades tóricas
Up: Curvas afines y proyectivas
Previous: Curvas afines y proyectivas
Contents
Index
Guillermo Morales-Luna
2011-10-19
![]() un polinomio irreducible y sea
Q
un polinomio irreducible y sea
Q![]() la curva que define. Sea
la curva que define. Sea
![]() el ideal generado por
el ideal generado por
![]() en el anillo
en el anillo
![]() , entonces
, entonces ![]() es primo y el cociente
es primo y el cociente
![]() es un dominio entero. Si
es un dominio entero. Si
![]() es un polinomio homogéneo de grado
es un polinomio homogéneo de grado ![]() , se dice que el elemento
, se dice que el elemento
![]() es una forma de grado
es una forma de grado ![]() . La colección de formas racionales sobre la curva
Q
es
. La colección de formas racionales sobre la curva
Q
es
![]() Q
y
Q
y
![]() un parámetro local en
un parámetro local en ![]() . Sea
. Sea
![]() Q
Q![]() una función racional tal que
una función racional tal que ![]() . Entonces existen
. Entonces existen
![]() y
y
![]() tales que
tales que ![]() . El entero
. El entero ![]() se dice ser la valuación de
se dice ser la valuación de ![]() en
en ![]() y se escribe
y se escribe
![]() . Se tiene que
. Se tiene que
![]() consiste de las funciones racionales con valuación no-negativa y
consiste de las funciones racionales con valuación no-negativa y
![]() de las racionales con valuación positiva.
de las racionales con valuación positiva.