



Next: Códigos de Goppa
Up: Divisores sobre curvas
Previous: Teorema de Riemann-Roch
Contents
Index
Sean
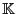 un campo y
Q
una curva. Un divisor monopuntual es uno donde su soporte es una mónada, es decir es de la forma
un campo y
Q
una curva. Un divisor monopuntual es uno donde su soporte es una mónada, es decir es de la forma
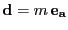 para algún punto
para algún punto
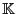 -racional
-racional
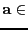 Q
,
Q
,
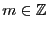 . En tal caso
. En tal caso
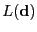 consta de las funciones
consta de las funciones
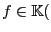 Q
Q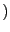 tales que
tales que
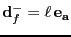 , con
, con
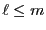 . Sea
. Sea
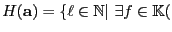
Q
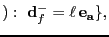
llamado el semigrupo de Weierstrass en 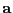 . Los enteros en
. Los enteros en
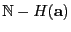 se dicen ser huecos para
se dicen ser huecos para 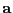 , y por mera contraposición, los de
, y por mera contraposición, los de
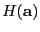 llenos para
llenos para 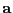 .
.
Proposición 5.1
Las siguientes aseveraciones son verdaderas:
- La dimensión del espacio
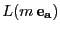 es el número de enteros llenos para
es el número de enteros llenos para 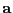 que no exceden
que no exceden 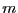 .
.
- Cualquier entero
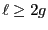 es lleno para todo
es lleno para todo
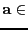 Q
.
Q
.
- En cada
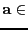 Q
hay exactamente
Q
hay exactamente 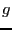 huecos para
huecos para 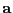 .
.
Lema 5.2
Sea
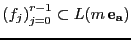 una sucesión de funciones racionales tales que las valuaciones
una sucesión de funciones racionales tales que las valuaciones
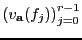 sean distintas a pares. Entonces las funciones
sean distintas a pares. Entonces las funciones
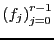 son linealmente independientes.
son linealmente independientes.




Next: Códigos de Goppa
Up: Divisores sobre curvas
Previous: Teorema de Riemann-Roch
Contents
Index
Guillermo Morales-Luna
2011-10-19
![]() un campo y
Q
una curva. Un divisor monopuntual es uno donde su soporte es una mónada, es decir es de la forma
un campo y
Q
una curva. Un divisor monopuntual es uno donde su soporte es una mónada, es decir es de la forma
![]() para algún punto
para algún punto
![]() -racional
-racional
![]() Q
,
Q
,
![]() . En tal caso
. En tal caso
![]() consta de las funciones
consta de las funciones
![]() Q
Q![]() tales que
tales que
![]() , con
, con
![]() . Sea
. Sea