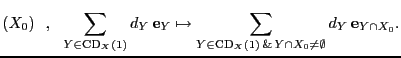Sea ![]() un espacio topológico y sea
un espacio topológico y sea
![]() un subespacio cerrado e irreducible. La codimensión de
un subespacio cerrado e irreducible. La codimensión de ![]() en
en ![]() es el supremo, menos 1, de las cardinalidades de cadenas crecientes de subespacios cerrados e irreducibles en
es el supremo, menos 1, de las cardinalidades de cadenas crecientes de subespacios cerrados e irreducibles en ![]() que se inician con
que se inician con ![]() .
.
Sea ![]() un anillo y sea
un anillo y sea ![]() un ideal primo. La codimensión de
un ideal primo. La codimensión de ![]() en
en ![]() es el supremo, menos 1, de las cardinalidades de cadenas decrecientes de ideales primos en
es el supremo, menos 1, de las cardinalidades de cadenas decrecientes de ideales primos en ![]() que se inician con
que se inician con ![]() , es pues su altura como se definió en la sección 2.1.1.
, es pues su altura como se definió en la sección 2.1.1.
Sea
CD![]() la colección de subespacios de codimensión 1 en
la colección de subespacios de codimensión 1 en ![]() . Un divisor de Weil en
. Un divisor de Weil en ![]() es un elemento del grupo libre
es un elemento del grupo libre
![]() :
:
![]() CD
CD![]() ; y
Weil
; y
Weil![]() es un grupo abeliano.
es un grupo abeliano.
Así, si ![]() es una curva entonces todo divisor de Weil es un divisor en el sentido de la sección anterior (cada mónada es de codimensión 1 en la curva).
es una curva entonces todo divisor de Weil es un divisor en el sentido de la sección anterior (cada mónada es de codimensión 1 en la curva).
Un divisor monopuntual también se dice ser un divisor irreducible. Un divisor efectivo es uno donde todos los valores ![]() son no-negativos.
son no-negativos.
![]() CD
CD![]() ,
, ![]() . El soporte del divisor
. El soporte del divisor
![]() es
Spt
es
Spt![]() . Si
. Si
![]() es un subespacio abierto de
es un subespacio abierto de ![]() entonces hay una inclusión natural
entonces hay una inclusión natural