




Next: Producto tensorial de álgebras
Up: Productos tensoriales
Previous: Productos tensoriales
Contents
Index
Sean 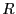 un anillo y
un anillo y 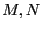 dos
dos 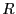 -módulos. Un
-módulos. Un 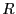 -módulo
-módulo 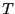 , junto con una transformación bilineal
, junto con una transformación bilineal
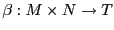 , es un producto tensorial de
, es un producto tensorial de 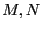 sobre
sobre 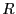 si satisface la siguiente Propiedad Universal del Producto Tensorial:
si satisface la siguiente Propiedad Universal del Producto Tensorial:
Para cualquier 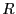 -módulo
-módulo 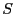 , si
, si
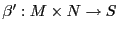 es una transformación bilineal entonces existe un único homomorfismo de
es una transformación bilineal entonces existe un único homomorfismo de 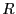 -módulos
-módulos
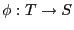 tal que
tal que
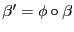 , es decir, que hace conmutativo el diagrama
, es decir, que hace conmutativo el diagrama
![$\displaystyle \xymatrix{ M\times N \ar[r]^{\beta} \ar[rd]_{\beta'} & T \ar@{.{>}}[d]^{\phi} \ & S }$](img144.png) |
(8) |
Una construcción directa consiste del 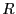 -módulo libre
-módulo libre
 , con la base natural
, con la base natural
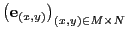 , reducido por el submódulo
, reducido por el submódulo 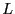 de
de
 generado por los elementos de las formas:
generado por los elementos de las formas:
con
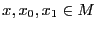 ,
,
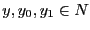 y
y 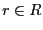 .
.
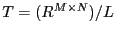 . La transformación
. La transformación 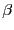 es la composición de funciones
es la composición de funciones
![$ (x,y)\mapsto {\bf e}_{(x,y)}\mapsto \pi({\bf e}_{(x,y)}) = [{\bf e}_{(x,y)}]$](img154.png) . Se denota, usualmente, al producto tensorial como
. Se denota, usualmente, al producto tensorial como
 (por lo general la transformación
(por lo general la transformación 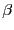 en general queda supuesta), y a los elementos en la base canónica se les escribe
en general queda supuesta), y a los elementos en la base canónica se les escribe
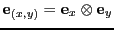 , por lo que cualquier elemento de
, por lo que cualquier elemento de
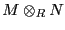 se expresa como
se expresa como
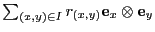 , con coeficientes
, con coeficientes
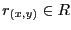 en el anillo
en el anillo 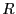 , para un conjunto finito
, para un conjunto finito
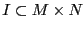 .
.
Proposición 1.6
Para cualquier 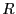 -módulo
-módulo  se tiene
se tiene
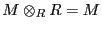 .
.
En efecto, consideremos la transformación bilineal dada por el producto por escalares,
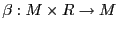 ,
,
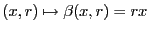 . Si
. Si 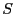 es un
es un 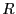 -módulo cualquiera y
-módulo cualquiera y
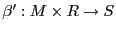 es una transformación bilineal, entonces
es una transformación bilineal, entonces
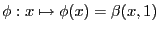 es el único
es el único 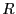 -homomorfismo
-homomorfismo  tal que
tal que
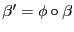 .
.
Proposición 1.7
El producto tensorial ``es'' conmutativo, asociativo y distributivo. Es decir, para cualesquiera 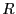 -módulos:
-módulos:
En efecto, estas relaciones se siguen de la propiedad universal (8).
Se dice que un complejo de 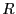 -módulos es una sucesión
-módulos es una sucesión
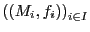 , donde
, donde
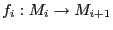 es un homomorfismo de
es un homomorfismo de 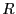 -módulos, tal que
-módulos, tal que 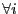 ,
,
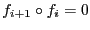 . Tal complejo se escribe más bien
. Tal complejo se escribe más bien
y se dice que es exacto si
img ker
ker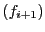 .
.
Así, se tiene que
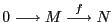 es exacta si y sólo si
es exacta si y sólo si 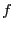 es inyectiva y
es inyectiva y
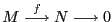 lo es si y sólo si
lo es si y sólo si 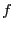 es suprayectiva.
es suprayectiva.
Proposición 1.8 (Exactitud derecha del producto tensorial)
Si se tiene una sucesión exacta
de 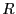 -módulos, entonces para cualquier
-módulos, entonces para cualquier 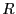 -módulo
-módulo 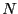 , es exacta la sucesión
, es exacta la sucesión
donde, para  ,
, 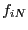 es el homomorfismo que hace conmutativo al diagrama
es el homomorfismo que hace conmutativo al diagrama





Next: Producto tensorial de álgebras
Up: Productos tensoriales
Previous: Productos tensoriales
Contents
Index
Guillermo Morales-Luna
2011-10-19
![]() un anillo y
un anillo y ![]() dos
dos ![]() -módulos. Un
-módulos. Un ![]() -módulo
-módulo ![]() , junto con una transformación bilineal
, junto con una transformación bilineal
![]() , es un producto tensorial de
, es un producto tensorial de ![]() sobre
sobre ![]() si satisface la siguiente Propiedad Universal del Producto Tensorial:
si satisface la siguiente Propiedad Universal del Producto Tensorial:
-módulo
, si
es una transformación bilineal entonces existe un único homomorfismo de
-módulos
tal que
, es decir, que hace conmutativo el diagrama
![]() ,
,
![]() . Si
. Si ![]() es un
es un ![]() -módulo cualquiera y
-módulo cualquiera y
![]() es una transformación bilineal, entonces
es una transformación bilineal, entonces
![]() es el único
es el único ![]() -homomorfismo
-homomorfismo ![]() tal que
tal que
![]() .
.
![]() -módulos es una sucesión
-módulos es una sucesión
![]() , donde
, donde
![]() es un homomorfismo de
es un homomorfismo de ![]() -módulos, tal que
-módulos, tal que ![]() ,
,
![]() . Tal complejo se escribe más bien
. Tal complejo se escribe más bien
![]() es exacta si y sólo si
es exacta si y sólo si ![]() es inyectiva y
es inyectiva y
![]() lo es si y sólo si
lo es si y sólo si ![]() es suprayectiva.
es suprayectiva.
![$\displaystyle \xymatrix{
M_i\times N \ar[d]_{\beta_i} \ar[r]^{(f_i,\mbox{\scrip...
...ar[d]^{\beta_{i+1}} \\
M_i\otimes_R N \ar[r]_{f_{iN}} & M_{i+1}\otimes_R N
}$](img186.png)