



Next: Variedades algebraicas
Up: Productos tensoriales
Previous: Producto tensorial de módulos
Contents
Index
Producto tensorial de álgebras
Sea 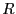 un anillo. Una
un anillo. Una 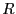 -álgebra es un anillo
-álgebra es un anillo 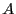 junto con un homomorfismo de anillos
junto con un homomorfismo de anillos
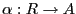 . En tal caso,
. En tal caso, 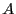 es también un
es también un 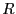 -módulo con el producto por escalares
-módulo con el producto por escalares
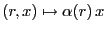 .
.
Sean 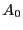 ,
, 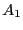 dos
dos 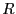 -álgebras. Una
-álgebras. Una 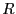 -álgebra
-álgebra 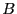 , junto con dos homomorfismos de
, junto con dos homomorfismos de 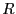 -álgebras
-álgebras
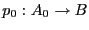 ,
,
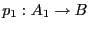 , es un producto tensorial de
, es un producto tensorial de 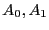 si satisface la siguiente Propiedad Universal del Producto Tensorial:
si satisface la siguiente Propiedad Universal del Producto Tensorial:
Para cualquier 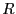 -álgebra
-álgebra 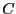 , y para cualesquiera dos homomorfismos de
, y para cualesquiera dos homomorfismos de 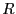 -álgebras
-álgebras
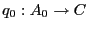 ,
,
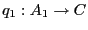 , existe un único homomorfismo de
, existe un único homomorfismo de 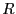 -álgebras
-álgebras
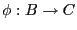 tal que
tal que
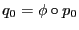 y
y
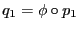 , es decir, que hace conmutativo el diagrama
, es decir, que hace conmutativo el diagrama
![$\displaystyle \xymatrix{ A_0 \ar[r]^{p_0} \ar[rd]_{q_0} & B \ar@{.{>}}[d]^{\phi} & A_1 \ar[l]_{p_1} \ar[ld]^{q_1} \ & C }$](img202.png) |
(9) |
Consideremos por un momento a las 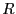 -álgebras
-álgebras 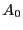 ,
, 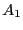 como
como 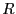 -módulos. Sea
-módulos. Sea
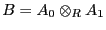 su producto tensorial de módulos. La transformación
su producto tensorial de módulos. La transformación
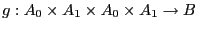 ,
,
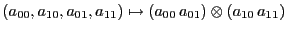 es multilineal, por lo cual puede factorizarse mediante una transformación bilineal
es multilineal, por lo cual puede factorizarse mediante una transformación bilineal
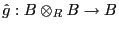 . Con este producto,
. Con este producto, 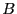 es una
es una 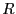 -álgebra, y junto con las funciones
-álgebra, y junto con las funciones
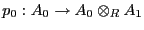 y
y
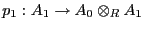 ,
,
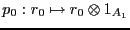 y
y
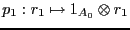 que son homomorfismos de
que son homomorfismos de 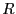 -álgebras, cumple con la propiedad universal (9).
Así pues, el producto tensorial de
-álgebras, cumple con la propiedad universal (9).
Así pues, el producto tensorial de 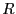 -álgebras es
-álgebras es
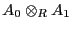 .
.




Next: Variedades algebraicas
Up: Productos tensoriales
Previous: Producto tensorial de módulos
Contents
Index
Guillermo Morales-Luna
2011-10-19
![]() un anillo. Una
un anillo. Una ![]() -álgebra es un anillo
-álgebra es un anillo ![]() junto con un homomorfismo de anillos
junto con un homomorfismo de anillos
![]() . En tal caso,
. En tal caso, ![]() es también un
es también un ![]() -módulo con el producto por escalares
-módulo con el producto por escalares
![]() .
.
![]() ,
, ![]() dos
dos ![]() -álgebras. Una
-álgebras. Una ![]() -álgebra
-álgebra ![]() , junto con dos homomorfismos de
, junto con dos homomorfismos de ![]() -álgebras
-álgebras
![]() ,
,
![]() , es un producto tensorial de
, es un producto tensorial de ![]() si satisface la siguiente Propiedad Universal del Producto Tensorial:
si satisface la siguiente Propiedad Universal del Producto Tensorial:
-álgebra
, y para cualesquiera dos homomorfismos de
-álgebras
,
, existe un único homomorfismo de
-álgebras
tal que
y
, es decir, que hace conmutativo el diagrama