



Siguiente: Problema de equivalencia (PE)
Un nivel arriba: Reducción de problemas al
Anterior: Problema de ``gramáticas ajenas''
Instancia:
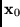
Solución:
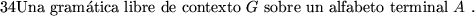
Proposición 3.4
PT es irresoluble.
Demostración: Puede verse que el lenguaje complementario a las representaciones trastocadas de computaciones en la máquina de Turing es libre de contexto. En efecto, una palabra 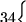 está en el lenguaje complementario si se cumple alguna de las condiciones siguientes:
está en el lenguaje complementario si se cumple alguna de las condiciones siguientes:
- 1.
- No es de la forma
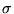 donde
donde
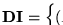 y
y
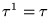 .
.
- 2.
- Siendo de la forma
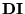 ,
se tiene que la primera
,
se tiene que la primera
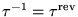 no es inicial (es decir, el q0 que ahí aparece no es el estado inicial de la máquina de Turing).
no es inicial (es decir, el q0 que ahí aparece no es el estado inicial de la máquina de Turing).
- 3.
- Siendo de la forma
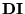 ,
se tiene que la última
,
se tiene que la última
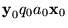 no es terminal, es decir,
no es terminal, es decir,
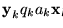 .
.
- 4.
- Para alguna i par se tiene
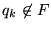 .
.
- 5.
- Para alguna i impar se tiene
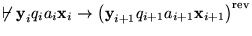 .
.
Cada una de las tres primeras condiciones define a un lenguaje regular, y por tanto, libre de contexto. La revisión de las condiciones 4. y 5. puede hacerse mediante sendos autómatas de pila y por tanto éstas determinan lenguajes libres de contexto. Así pues, el lenguaje complementario es libre de contexto como unión de lenguajes libres de contexto.
Si pudiéramos reconocer que este lenguaje es total podríamos reconocer que no hay computación terminal para una entrada dada de la máquina de Turing. Esto también resolvería el Problema de la Parada.




Siguiente: Problema de equivalencia (PE)
Un nivel arriba: Reducción de problemas al
Anterior: Problema de ``gramáticas ajenas''
Guillermo Morales-Luna
2000-07-10