next up previous contents
Siguiente: Problema de totalidad (PT) Un nivel arriba: Reducción de problemas al Anterior: Reducción de problemas al

Problema de ``gramáticas ajenas'' (PA)




Instancia:
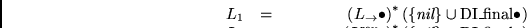
\begin{pagi}{34}Dos gram\'aticas libres de contexto $G_1, G_2$\space con un mismo alfabeto terminal $A$ .\end{pagi}
Solución:
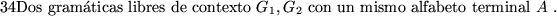
\begin{pagi}{34}$\left\{\begin{array}{ll} 1 &\mbox{\rm si $G_1\cap G_2=\emptyset$ , } \\ 0 &\mbox{\rm en otro caso. } \end{array}\right.$\end{pagi}



Proposición 3.3   PA es irresoluble.

Demostración: Si pudiéramos decidir cuándo dos lenguajes libres de contexto tienen intersección no-vacía, al considerar los lenguajes L1 y L2 de la proposición anterior podríamos decidir si la máquina M posee una computación terminal a partir de 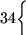$\mbox{\bf x}_0$. Así pues resolveríamos el Problema de la Parada para máquinas de Turing. Como esto es imposible, PA es irresoluble.
Guillermo Morales-Luna
2000-07-10