- 1.
-
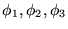 .
.
- 2.
-
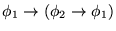 .
.
- 3.
-
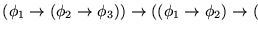 .
.
- 4.
-
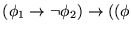 .
.
Con esto, sea P- el conjunto de los siguientes axiomas propios:
Sea
 ,
donde EI es el esquema de inducción:
,
donde EI es el esquema de inducción:
 ,
donde EI es el esquema de inducción:
,
donde EI es el esquema de inducción:
Modus Ponens. Cualesquiera que sean las fórmulas
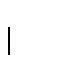 : :
|
Generalización. Cualquiera que sea la fórmula 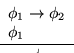
|
![$D=[\delta_0,\ldots,\delta_m]$](img1215.gif) de fórmulas bien formadas tal que
de fórmulas bien formadas tal que