



Siguiente: Teoremas de jerarquía
Un nivel arriba: Clasificación de problemas irresolubles
Anterior: Computaciones con oráculos
Enumerabilidad recursiva relativa a oráculos
En esta parte introduciremos algunas nociones básicas que presentaremos (Cfr 7.1.1) más adelante. Veremos aquí que los problemas irresolubles mediante funciones computables son heredados por clases de funciones que extienden a las computables mediante oráculos.
Dados dos conjuntos A,B,
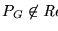 ,
diremos que
De manera natural se tiene que las siguientes proposiciones son válidas:
,
diremos que
De manera natural se tiene que las siguientes proposiciones son válidas:
Proposición 5.3
La relación ``
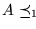
'' es reflexiva y transitiva.
En efecto, es reflexiva porque la función identidad es computable. Es transitiva, porque la clase de funciones computables es cerrada bajo composición de funciones.
Proposición 5.4
``
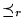
'' es un refinamiento de ``
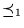
'' y ``
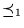
'' es un refinamiento de ``
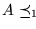
'', es decir
En efecto, la condición que define a ``
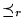 '' es más fuerte que la de ``
'' es más fuerte que la de ``
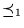 '', pues aquella exige que la función f tal que
A=f-1(B) sea inyectiva. por otro lado, si
A=f-1(B), donde f es computable, entonces
'', pues aquella exige que la función f tal que
A=f-1(B) sea inyectiva. por otro lado, si
A=f-1(B), donde f es computable, entonces
 ,
es decir
,
es decir 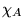 es recursiva respecto a
es recursiva respecto a 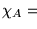 .
.
Proposición 5.5
Las relaciones ``
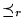
'' y ``
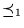
'' son reflexivas y transitivas.
En efecto, la función identidad es computable y la composición de computables es computable.
Toda relación entre conjuntos que sea reflexiva y transitiva se dice ser una reducibilidad.
Sea 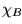 una clase de conjuntos y ``
una clase de conjuntos y ``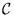 '' una reducibilidad.
'' una reducibilidad.
- La clase
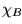 es cerrada respecto a la reducibilidad ``
es cerrada respecto a la reducibilidad ``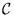 '' si
'' si
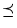
- Un conjunto B es difícil para la clase
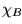 si
si
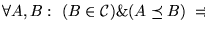
- Un conjunto B es completo para la clase
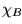 (completo-
(completo-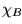 )
si además de ser difícil para la clase
)
si además de ser difícil para la clase 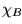 está también en la clase
está también en la clase 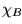 .
.
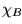 es cerrada-m o cerrada-1 si es cerrada respecto a la reducibilidad
es cerrada-m o cerrada-1 si es cerrada respecto a la reducibilidad 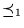 o
o 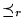 respectivamente.
respectivamente.
Sea G una función total.
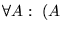 es recursivamente enumerable-G, r.e.-G, si es el dominio de una función recursiva-G.
Como en el caso sin oráculos se tiene las propiedades siguientes:
es recursivamente enumerable-G, r.e.-G, si es el dominio de una función recursiva-G.
Como en el caso sin oráculos se tiene las propiedades siguientes:
Proposición 5.6
Si B es recursivo-G entonces B es r.e.-G.
Proposición 5.7
B es recursivo-G si y sólo si ambos B y Bc son r.e.-G.
Proposición 5.8
La clase de conjuntos r.e.-G es cerrada bajo las operaciones conjuntistas de unión e intersección.
Proposición 5.9
Los conjuntos r.e.-G son las proyecciones de las relaciones recursivas-G.
Proposición 5.10
Sea
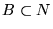
una enumeración de las funciones recursivas-
G. Sean
Entonces ambos conjuntos

son r.e.-
G mas no son recursivos-
G.
Proposición 5.11
Para cada conjunto
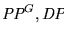
,
las siguientes condiciones son equivalentes a pares:
- 1.
- A es r.e.-G.
- 2.
-
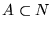 .
.
- 3.
-
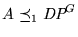 .
.
Proposición 5.12
Para cada función total
G, las sucesiones de conjuntos

y de funciones
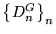
definidas simultáneamente de manera recursiva:
definen una jerarquía de ``irresolubilidades''.




Siguiente: Teoremas de jerarquía
Un nivel arriba: Clasificación de problemas irresolubles
Anterior: Computaciones con oráculos
Guillermo Morales-Luna
2000-07-10
 .
.
 .
.
 ,
es decir
,
es decir  son r.e.-G mas no son recursivos-G.
son r.e.-G mas no son recursivos-G.