



Siguiente: Problemas difíciles y completos
Un nivel arriba: Clases de problemas
Anterior: Clases de problemas
Reducibilidades
Recordemos algunas de las nociones introducidas en la sección 5.5.2. Ahí convinimos en que para dos conjuntos de números naturales, A,B no vacíos,
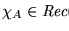 denota que
denota que
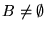 ,
,
 denota que existe una función computable f tal que
A=f-1(B) y, finalmente,
denota que existe una función computable f tal que
A=f-1(B) y, finalmente,
 denota que existe una función computable e inyectiva f tal que
A=f-1(B). Las relaciones ``
denota que existe una función computable e inyectiva f tal que
A=f-1(B). Las relaciones ``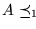 '', ``
'', ``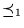 '' y ``
'' y ``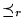 '' son reducibilidades, es decir, son reflexivas y transitivas, y cada una es un refinamiento de la anterior.
De manera más general, si
'' son reducibilidades, es decir, son reflexivas y transitivas, y cada una es un refinamiento de la anterior.
De manera más general, si 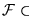 es una familia de funciones, escribiremos
es una familia de funciones, escribiremos
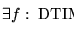 para denotar que existe una función
para denotar que existe una función
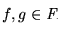 tal que
A=f-1(B). Obviamente, ``
tal que
A=f-1(B). Obviamente, ``
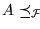 '' es reducibilidad si, por ejemplo, la familia
'' es reducibilidad si, por ejemplo, la familia 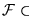 contiene a la identidad y es cerrada bajo composición.
Si ``
contiene a la identidad y es cerrada bajo composición.
Si ``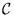 '' es una reducibilidad, ésta induce a la relación ``
'' es una reducibilidad, ésta induce a la relación ``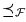 '' definida como sigue:
'' definida como sigue:
Proposición 1.1
``
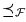
'' es una relación de equivalencia.
Sea 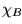 una clase de conjuntos y ``
una clase de conjuntos y ``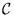 '' una reducibilidad.
'' una reducibilidad.
Proposición 1.2
Sea
A un conjunto completo en la clase
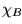
y sea
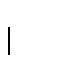
tal que
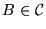
.
Entonces
B es completo en la clase
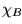
.
Definamos
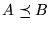 De manera inmediata, se tiene las siguientes proposiciones:
De manera inmediata, se tiene las siguientes proposiciones:
Proposición 1.3
Si
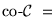
fuera cerrado y hubiera un conjunto
A completo para
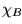
que estuviera también en
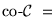
entonces se ha de tener
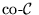
En efecto, bajo las hipótesis hechas se prueba fácilmente que
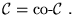 .
De manera completamente simétrica se prueba la inclusión opuesta.
.
De manera completamente simétrica se prueba la inclusión opuesta.
Proposición 1.4
Si

entonces
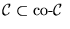
.
También:
Si
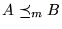
entonces
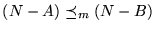
.
En efecto, si
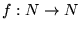 es tal que
A=f-1(B), evidentemente se tendrá también que
(N-A)=f-1(N-B).
es tal que
A=f-1(B), evidentemente se tendrá también que
(N-A)=f-1(N-B).
Proposición 1.5
Si
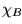
fuera cerrada-
m o cerrada-1 entonces también lo es
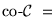
.
Esto es una consecuencia de la proposición anterior.
Proposición 1.6
Sea
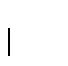
una enumeración de las funciones recursivas y sea
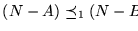
Entonces,
K es completo-1 para la clase de conjuntos recursivamente enumerables.
En efecto, sea A recursivamente enumerable. Hemos de probar que para alguna función recursiva e inyectiva f0 se tiene
A=f0-1(K).
Como A es recursivamente enumerable existe una función recursiva fA cuyo dominio es precisamente A. Consideremos la función recursiva,
Por el Teorema de Parametrización, existe una función recursiva f0 tal que
 Observemos que las funciones de la forma
Observemos que las funciones de la forma
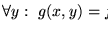 son todas constantes. Por tanto el predicado
son todas constantes. Por tanto el predicado
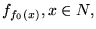 es recursivo. Así pues, se puede modificar fácilmente a f0 de manera que sea inyectiva si acaso no lo fuera ya.
Se cumplen además las equivalencias siguientes:
es recursivo. Así pues, se puede modificar fácilmente a f0 de manera que sea inyectiva si acaso no lo fuera ya.
Se cumplen además las equivalencias siguientes:
Proposición 1.7
Si A es un conjunto completo-m para la clase de conjuntos recursivamente enumerables entonces su complemento Ac no puede ser recursivamente enumerable.
Se tiene que la clase de los conjuntos recursivamente enumerables es cerrada-m. Luego, si Ac fuera recursivamente enumerable entonces el complemento de todo recursivamente enumerable también sería recursivamente enumerable. Evidentemente, esta última propiedad no puede ser cierta.
Proposición 1.8
Dados,

sea
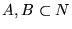
Entonces,
- 1.
-
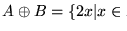 .
.
- 2.
-
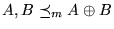
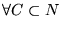 es el conjunto que contiene la información de ambos A y B y nada más.
es el conjunto que contiene la información de ambos A y B y nada más.




Siguiente: Problemas difíciles y completos
Un nivel arriba: Clases de problemas
Anterior: Clases de problemas
Guillermo Morales-Luna
2000-07-10
 denota que existe una función computable f tal que
A=f-1(B) y, finalmente,
denota que existe una función computable f tal que
A=f-1(B) y, finalmente,
 denota que existe una función computable e inyectiva f tal que
A=f-1(B). Las relaciones ``
denota que existe una función computable e inyectiva f tal que
A=f-1(B). Las relaciones ``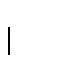 tal que
tal que
 entonces
entonces
 una enumeración de las funciones recursivas y sea
una enumeración de las funciones recursivas y sea
 Observemos que las funciones de la forma
Observemos que las funciones de la forma
 sea
sea