



Siguiente: Funciones logarítmicas
Un nivel arriba: Algunas clases de funciones
Anterior: Funciones polinomiales
Sean a,b>0. Tenemos que
Y por tanto,
 Sin embargo, como
Sin embargo, como
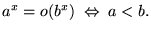 se tiene
se tiene
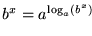 En este sentido, es irrelevante el tamaño de la base de exponenciación, la cual puede ser 2, e o 10.
La clase de funciones con crecimiento exponencial es pues
En este sentido, es irrelevante el tamaño de la base de exponenciación, la cual puede ser 2, e o 10.
La clase de funciones con crecimiento exponencial es pues
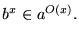 Por otro lado, la serie de Taylor de la función exponencial es
Por otro lado, la serie de Taylor de la función exponencial es
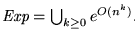 Luego,
Luego,
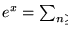
por lo cual
es decir,
xk=o(ex).
En otras palabras, la función exponencial domina asintóticamente a cualquier polinomial.
Guillermo Morales-Luna
2000-07-10


 Sin embargo, como
Sin embargo, como