



Siguiente: Funciones polilogarítmicas
Un nivel arriba: Algunas clases de funciones
Anterior: Funciones exponenciales
Sean a,b>0. Tenemos que
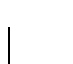 :
:
 Por tanto
Por tanto
 Así pues podemos considerar al logaritmo natural
Así pues podemos considerar al logaritmo natural
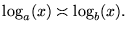 como representativa de la clase de las funciones con crecimiento logarítmico
como representativa de la clase de las funciones con crecimiento logarítmico
 La función logaritmo está dominada asintóticamente por la identidad. En efecto, como
La función logaritmo está dominada asintóticamente por la identidad. En efecto, como
tenemos que el cociente
 es estrictamente decreciente, y positivo, en el intervalo
es estrictamente decreciente, y positivo, en el intervalo
![$]e,+\infty[$](img1465.gif) .
En particular para la sucesión de puntos xn=en tenemos
.
En particular para la sucesión de puntos xn=en tenemos
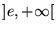 Así pues
Así pues
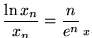 .
.
Guillermo Morales-Luna
2000-07-10
 :
:
 es estrictamente decreciente, y positivo, en el intervalo
es estrictamente decreciente, y positivo, en el intervalo