Siguiente: El primer problema completo-NP
Un nivel arriba: Formas proposicionales y el
Anterior: Formas proposicionales y el
Utilizaremos los siguientes símbolos constantes
- 1: Valor verdadero. Es la unidad de ``
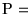 '':
'':
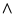 .
.
- 0: Valor falso. Es la unidad de ``
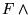 '':
'':
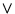 .
.
Sea
![$\mbox{\bf X}=\left[X_j\right]_{j=1,\ldots,n_0}$](img1640.gif) una lista de variables.
Consideremos las siguientes estructuras sintácticas:
una lista de variables.
Consideremos las siguientes estructuras sintácticas:
- Literales
- Variables o negaciones de variables:
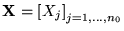
- Cláusulas
- Disyunciones de literales: Para cada
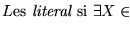 hacemos
hacemos
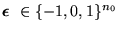 donde
donde
En una cláusula
 tenemos
tenemos
- Frases
- Conjunciones de literales: Para cada
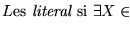 hacemos
hacemos
 donde
donde
Como en el caso de las cláusulas
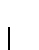 indica cuáles variables aparecen en la frase, y en este caso indica a su signo de aparición.
indica cuáles variables aparecen en la frase, y en este caso indica a su signo de aparición.
- Formas conjuntivas
- Conjunciones de cláusulas. Si
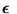 entonces representamos a
entonces representamos a
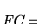 por la matriz
por la matriz
![$\mbox{\it FC}=\left[L_{ij}\right]_{i,j}^C$](img1652.gif) .
.
- Formas disyuntivas
- Disyunciones de frases. Si
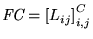 entonces representamos a
entonces representamos a
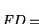 por la matriz
por la matriz
![$\mbox{\it FD}=\left[L_{ij}\right]_{i,j}^D$](img1655.gif) .
.
- Formas proposicionales
- Puesto recursivamente,
-
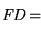 son formas proposicionales.
son formas proposicionales.
- Las variables son formas proposicionales.
- Las negaciones de formas proposicionales son también formas proposicionales.
- Las conjunciones y las disyunciones de formas proposicionales son también formas proposicionales.
Sea
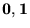 el conjunto de los dos valores de verdad booleanos. Toda forma proposicional F determina una función
el conjunto de los dos valores de verdad booleanos. Toda forma proposicional F determina una función
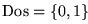 .
Para cada
.
Para cada
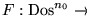
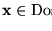 es el valor de verdad que asume F bajo la asignación
es el valor de verdad que asume F bajo la asignación
 .
Dos formas son equivalentes si definen a una misma función.
Confundiremos voluntariamente a una forma proposicional con la función
.
Dos formas son equivalentes si definen a una misma función.
Confundiremos voluntariamente a una forma proposicional con la función
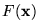 que define.
Una forma proposicional F es
que define.
Una forma proposicional F es
- satisfactible si hay una asignación que la satisface, es decir, si
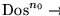 ,
,
- tautología si es satisfecha por todas las posibles asignaciones, es decir, si
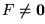 ,
,
- refutable si hay una asignación que la refuta, es decir, si
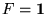 ,
,
- insatisfactible si es refutada por todas las posibles asignaciones, es decir, si
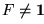 .
.




Siguiente: El primer problema completo-NP
Un nivel arriba: Formas proposicionales y el
Anterior: Formas proposicionales y el
Guillermo Morales-Luna
2000-07-10
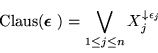
 tenemos
tenemos
 donde
donde