



Siguiente: Otros problemas completos-NP en
Un nivel arriba: Formas proposicionales y el
Anterior: Formas booleanas
- Problema SAT
- Consiste en decidir si acaso una forma proposicional dada es satisfactible.
Formalmente el problema se especifica como sigue:
Instancia:
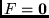
Solución:
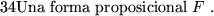
Toda instancia
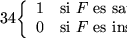 de SAT puede verse como una palabra sobre el alfabeto
de SAT puede verse como una palabra sobre el alfabeto
de n0+7 símbolos. Si la longitud de esta palabra es n tenemos que
- 1.
- hay a lo sumo
 apariciones de variables,
apariciones de variables,
- 2.
- la cadena se codifica como una palabra de longitud
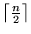 sobre el alfabeto
sobre el alfabeto 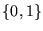 .
En efecto,
.
En efecto,
- (a)
- a cada variable Xj la codificamos por la palabra formada por un símbolo x seguido de la representación de j en base 2. Digamos,
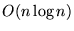 .
.
- (b)
- codifiquemos a cada uno de los símbolos en uso actual como se indica en la Tabla 7.1.
Table 7.1:
Codificación de símbolos.
| Símbolo |
Código |
Símbolo |
Código |
| ( |
1 |
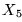 |
110 |
| ) |
10 |
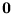 |
111 |
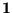 |
11 |
x |
1000 |
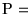 |
100 |
0 |
1001 |
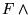 |
101 |
1 |
1010 |
|
- (c)
- cada cadena en el lenguaje proposicional se transcribe como una cadena de cadenas de 0's y 1's. V.gr,:
- (d)
- A una cadena de cadenas de 0's y 1's. la representamos, mediante una sola cadena de 0's y 1's, cambiando cada 1 por 10, cada 0 por 0 mismo y cada ``,'' por 11. V.gr,:
- 3.
- Consecuentemente, respecto a reducciones en espacio logarítmico es irrelevante utilizar el alfabeto
 o el alfabeto
o el alfabeto 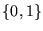 pues
pues
Lo mismo vale respecto a reducciones polinomiales.
Teorema 3.1 (Cook, 1971)
SAT es completo-NP.
Demostración: Veamos primeramente que
 .
Dada una instancia
.
Dada una instancia
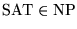 ,
se genera una asignación
,
se genera una asignación
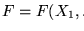 de manera no determinista. La evaluación de F sobre
de manera no determinista. La evaluación de F sobre
 requiere un tiempo proporcional al número de conectivos que aparecen en F el cual está limitado por la propia longitud de F.
Veamos ahora que
requiere un tiempo proporcional al número de conectivos que aparecen en F el cual está limitado por la propia longitud de F.
Veamos ahora que
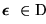 es difícil-
es difícil-
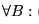 .
Para esto, hay que ver que cualquier problema en NP se reduce a SAT, para lo cual veremos que para cualquier máquina de Turing no-determinista M, acotada en tiempo por un polinomio p(n), podemos construir un traductor logarítmico
.
Para esto, hay que ver que cualquier problema en NP se reduce a SAT, para lo cual veremos que para cualquier máquina de Turing no-determinista M, acotada en tiempo por un polinomio p(n), podemos construir un traductor logarítmico
de manera que
 Consideremos una computación terminal en M, correspondiente a una entrada
Consideremos una computación terminal en M, correspondiente a una entrada
 de longitud n. Esta es una sucesión finita de descripciones instantáneas cuya longitud es O(p(n)). Escribámosla
de longitud n. Esta es una sucesión finita de descripciones instantáneas cuya longitud es O(p(n)). Escribámosla
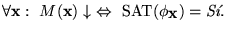 Cada
Cada
![$\mbox{\it di}_i=[\mbox{\bf x}_iq_ia_i\mbox{\bf y}_i]$](img1687.gif) involucra del orden de p(n) símbolos. De hecho, podemos confundir a la pareja qiai como un solo símbolo (nuevo) qiaimi, donde mi indica al movimiento que hace M estando en el estado qi y encontrando el símbolo ai.
Así, se puede escribir la computación
involucra del orden de p(n) símbolos. De hecho, podemos confundir a la pareja qiai como un solo símbolo (nuevo) qiaimi, donde mi indica al movimiento que hace M estando en el estado qi y encontrando el símbolo ai.
Así, se puede escribir la computación
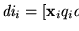 como una palabra de longitud
(p(n)+1)2 sobre un cierto alfabeto A'.
Consideremos el conjunto de variables proposicionales
como una palabra de longitud
(p(n)+1)2 sobre un cierto alfabeto A'.
Consideremos el conjunto de variables proposicionales
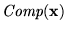 La intención de cada una de estas variables es
La intención de cada una de estas variables es
La construcción de
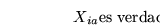 se hará teniendo en mente lo siguiente:
se hará teniendo en mente lo siguiente:
- 1.
- Para cada i existe un único a tal que Xia es verdadero.
- 2.
- La descripción inicial
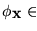 es de la forma
es de la forma
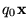 .
.
- 3.
- La última descripción
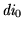 es terminal.
es terminal.
- 4.
- Cada descripción
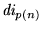 se sigue de su anterior
se sigue de su anterior
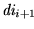 según las transiciones de la máquina M.
según las transiciones de la máquina M.
De acuerdo con el punto 1 anterior definamos
![\begin{displaymath}\phi_{1,\mbox{\bf x}}=\bigwedge_{i}\left[\bigvee_{a}\left(X_{ia}\land\bigwedge_{b\not=a}\neg X_{ib}\right)\right].
\end{displaymath}](img1696.gif) |
(16) |
De acuerdo con el punto 2 anterior consideremos lo siguiente:
- La descripción inicial
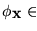 ,
como cualquier otra, va entre dos ``
,
como cualquier otra, va entre dos `` '''s. Sea
'''s. Sea
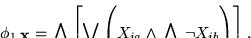 |
(17) |
- El primer símbolo de
 corresponde al símbolo compuesto formado por el estado inicial q0 de M y el símbolo inicial x1 de
corresponde al símbolo compuesto formado por el estado inicial q0 de M y el símbolo inicial x1 de
 .
Sea
.
Sea
![\begin{displaymath}\phi_{2,2,\mbox{\bf x}}=\bigvee_{[q_0x_1m]\in\mbox{\rm Transiciones en $M$ }}X_{1[q_0x_1m]}.
\end{displaymath}](img1698.gif) |
(18) |
- Los siguientes n-1 símbolos de
 corresponden a los símbolos xi que conforman a
corresponden a los símbolos xi que conforman a
 .
Sea
.
Sea
 |
(19) |
- El resto de
 se llena con blancos. Sea
se llena con blancos. Sea
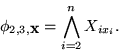 |
(20) |
Tomemos pues a la conjunción de las fórmulas en las ecuaciones 7.2-7.5:
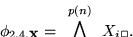 |
(21) |
De acuerdo con el punto 3 anterior definamos
![\begin{displaymath}\phi_{3,\mbox{\bf x}}=\bigvee_{i=p(n)(p(n)+1)+1}^{(p(n)+1)^2-...
...in&\mbox{\rm Transiciones}\end{array}
}X_{i[q_Fam]}\right].
\end{displaymath}](img1702.gif) |
(22) |
Finalmente, para expresar la necesidad de que dos descripciones contiguas
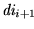 y
y
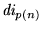 se ajustan a las transiciones de M, observamos que tales dos descripciones han de coincidir en todas partes salvo en las posiciones vecinas a los símbolos compuestos correspondientes a estados. Definamos entonces un predicado
se ajustan a las transiciones de M, observamos que tales dos descripciones han de coincidir en todas partes salvo en las posiciones vecinas a los símbolos compuestos correspondientes a estados. Definamos entonces un predicado
 tal que
tal que
Con 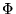 podemos simular efectivamente las transiciones de M.
Sea entonces
podemos simular efectivamente las transiciones de M.
Sea entonces
![\begin{displaymath}\phi_{4,\mbox{\bf x}}=\bigwedge_{j=1}^{p(n)(p(n)+1)}\bigvee_{...
...(j),a_2}\land X_{(j+1),a_3}\land X_{(p(n)+j),a_4}
\right].
\end{displaymath}](img1705.gif) |
(23) |
La forma proposicional a construir es entonces la conjunción de las fórmulas 7.1, 7.6, 7.7 y 7.8:
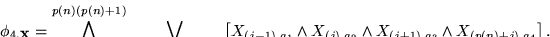 |
(24) |
De su misma construcción tenemos que toda computación terminal, con inicio en
 ,
determina una asignación que satisface a la fórmula
,
determina una asignación que satisface a la fórmula
 y, viceversa, toda asignación que satisfaga a esta fórmula determina también a una computación terminal a partir de
y, viceversa, toda asignación que satisfaga a esta fórmula determina también a una computación terminal a partir de
 .
.




Siguiente: Otros problemas completos-NP en
Un nivel arriba: Formas proposicionales y el
Anterior: Formas booleanas
Guillermo Morales-Luna
2000-07-10
 apariciones de variables,
apariciones de variables,
 o el alfabeto
o el alfabeto  .
Dada una instancia
.
Dada una instancia
 tal que
tal que