



Siguiente: Problemas de asignación de
Un nivel arriba: Algunos problemas principales completos-NP
Anterior: Partición
Una gráfica es un sistema G=(V,A) donde
-
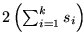 es un conjunto de vértices o nodos, y
es un conjunto de vértices o nodos, y
-
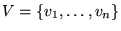 es un conjunto de aristas (sin dirección).
es un conjunto de aristas (sin dirección).
Una gráfica se dice ser
- un clan o completa si contiene todas las
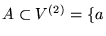 aristas posibles, y en tal caso se le denota como Kn,
aristas posibles, y en tal caso se le denota como Kn,
- vacía o independiente si su conjunto de aristas es vacío, y en tal caso la denotaremos por In.
El complemento, o gráfica complementaria, de una gráfica G=(V,A) es
Gc=(V,V(2)-A), es decir
Así, por ejemplo, Kn e In son gráficas complementarias una de otra.
Recordamos también los conceptos siguientes:
- un recubrimiento por vértices es un subconjunto
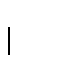 de vértices tal que toda arista tiene al menos un extremo en él, es decir, tal que
de vértices tal que toda arista tiene al menos un extremo en él, es decir, tal que
- un recubrimiento por aristas es un subconjunto
 de aristas tal que todo vértice está en al menos una de tales aristas, es decir, tal que
de aristas tal que todo vértice está en al menos una de tales aristas, es decir, tal que
Consideremos los siguientes problemas:
Recubrimiento por vértices (VC): Este problema (vertex cover) se describe como sigue:
Instancia:

Solución:
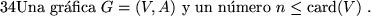
Clan (CLIQUE):
Instancia:

Solución:

Conjunto independiente:
Instancia:

Solución:
Los tres problemas anteriores se reducen entre sí debido al evidente
Lema: Para una gráfica G=(V,A) y un subconjunto
 las siguientes tres condiciones son equivalentes a pares:
las siguientes tres condiciones son equivalentes a pares:
- 1.
- U es un recibrimiento por vértices de G.
- 2.
- V-U es un conjunto independiente en G.
- 3.
- V-U es un clan en la gráfica complementaria Gc.
Proposición: VC es completo-NP.
Demostración: VC es naturalmente un problema en la clase NP.
Para ver que es difícil-NP reduciremos 3SAT a VC.
Dados
-
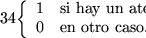 :
conjunto de n variables proposicionales,
:
conjunto de n variables proposicionales,
-
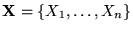 :
conjunto de m cláusulas de 3 literales sobre
:
conjunto de m cláusulas de 3 literales sobre
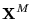 ,
,
construiremos una instancia de VC de manera que ésta dé una instancia con respuesta positiva en VC si y sólo si la forma conjuntiva
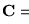 es satisfactible. En tal caso, un recubrimiento por vértices de la instancia construída ha de determinar una asignación de valores de verdad a las variables en
es satisfactible. En tal caso, un recubrimiento por vértices de la instancia construída ha de determinar una asignación de valores de verdad a las variables en
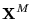 que satisfaga a
que satisfaga a
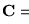 .
Definamos
.
Definamos
- para cada variable
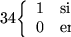 ,
una gráfica consistente de una sola arista,
,
una gráfica consistente de una sola arista,
- para cada cláusula
 ,
una gráfica consistente de un triángulo,
,
una gráfica consistente de un triángulo,
y
- para cada cláusula, que consta de tres literales,
tendemos las aristas de los vértices de Gi a los correspondientes vértices ``literales'' de las gráficas de la forma Gj siguientes
Así pues, la gráfica construída G=(V,A) consta de 2n+3m vértices y n+6m aristas.
- Finalmente, hagamos N=n+2m.
Una solución de 3SAT da una solución de VC: Supongamos que
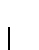 es una asignación que satisface a C. Construyamos el recubrimiento U siguiente:
es una asignación que satisface a C. Construyamos el recubrimiento U siguiente:
- Para cada
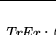 ,
,
- Como la asignación
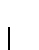 satisface a cada una de las cláusulas ci tenemos que para toda Gi uno de los vértices ``queda cubierto'', es decir, es el extremo de una arista cuyo otro extremo ha quedado en U. Fijamos pues en cada triángulo Gi un vértice cubierto y los otros dos los incluimos en U.
satisface a cada una de las cláusulas ci tenemos que para toda Gi uno de los vértices ``queda cubierto'', es decir, es el extremo de una arista cuyo otro extremo ha quedado en U. Fijamos pues en cada triángulo Gi un vértice cubierto y los otros dos los incluimos en U.
- Tenemos así un recubrimiento por vértices con K vértices.
Una solución de VC da una solución de 3SAT: Si U es un recubrimiento por vértices con n+2m vértices entonces en cada arista Gj exactamente uno de sus extremos pertenece a U. Hagamos verdadera a la literal correspondiente al extremo en U, en cada Gj. Esta asignación evidentemente satisface a cada cláusula.




Siguiente: Problemas de asignación de
Un nivel arriba: Algunos problemas principales completos-NP
Anterior: Partición
Guillermo Morales-Luna
2000-07-10
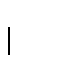 de vértices tal que toda arista tiene al menos un extremo en él, es decir, tal que
de vértices tal que toda arista tiene al menos un extremo en él, es decir, tal que
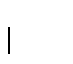 de aristas tal que todo vértice está en al menos una de tales aristas, es decir, tal que
de aristas tal que todo vértice está en al menos una de tales aristas, es decir, tal que
 las siguientes tres condiciones son equivalentes a pares:
las siguientes tres condiciones son equivalentes a pares:
 ,
una gráfica consistente de un triángulo,
,
una gráfica consistente de un triángulo,