next up previous contents
Siguiente: Problemas en gráficas Un nivel arriba: Combinatoria Anterior: Atercetamientos (3DM):

Partición

Consideremos el problema siguiente


Instancia:
\begin{pagi}{34}Una sucesi\'on $\mbox{\bf s}=[s_1,\ldots,s_n]\in N^n$ .\end{pagi}
Solución:
\begin{pagi}{34}$\left\{\begin{array}{ll} 1 &\mbox{\rm si existe $I\subset[1,n]... ...in I}}s_i$ , } \\ 0 &\mbox{\rm en otro caso. } \end{array}\right.$\end{pagi}



Es claro que este problema PARTITION está en NP. Para ver que es difícil-NP veamos que 3DM se reduce a él. Sea $M=[m_1,\ldots,m_k]\subset X\times Y\times Z$ una instancia de 3DM, con

\begin{eqnarray*}X &=& [x_1,\ldots,x_q] \\ Y &=& [y_1,\ldots,y_q] \\ Z &=& [z_1,\ldots,z_q] \\ k &\geq& q \end{eqnarray*}


Construiremos una instancia $\mbox{\bf s}=[s_1,\ldots,s_n]\in N^n$ de PARTITION tal que

\begin{displaymath}\left[\exists I\subset[1,n]:\sum_{i\in I}s_i=\sum_{i\not\in I... ...m}$M'$ es un aterceta\-mien\-to de $q$ tercetas.\end{minipage}}\end{displaymath}

Consideremos pues los siguientes conceptos:

\begin{eqnarray*}n=k+2 &:&\mbox{\rm\begin{minipage}[t]{22em} n\'umero de sumand... ...{f(i)},y_{g(i)},z_{h(i)}].\end{displaymath} \end{minipage}} \\ \end{eqnarray*}


Para cada $i=1,\ldots,k$ sea

\begin{displaymath}s_i=\left(2^p\right)^{(3q-f(i))} + \left(2^p\right)^{(2q-g(i))} + \left(2^p\right)^{(q-h(i))}.\end{displaymath}

Cada si está determinado por la terceta mi, así, escribiremos también s(mi)=si. Tenemos entonces que cada sumando de la sucesión $\mbox{\bf s}$ se escribe con exactamente 3pq bits. En la Figura 8.1 presentamos diagramáticamente esta construcción.
  
Figure: Construcción de los sumandos en $\mbox{\bf s}$.
\fbox{\begin{minipage}[t]{29em} \begin{displaymath}\underbrace{ \underbrace{\c... ...i)}$\space y $z_{h(i)}$ , y tiene 0's en las dem\'as posiciones. \end{minipage}}

Sea B el número con 1 en las posición más a la derecha de cada segmento de p bits,

\begin{displaymath}B=\sum_{i=0}^{3q-1}\left(2^p\right)^{i}.\end{displaymath}

Entonces, para todo subconjunto de tercetas $M'\subset M$ se cumple que

\begin{displaymath}\sum_{m\in M'}s(m)=B\ \Leftrightarrow\ M'\mbox{\rm es un atercetamiento}.\end{displaymath}

Finalmente definamos

\begin{displaymath}\begin{array}{ccc} s_{k+1}=2\left(\sum_{i=1}^k s_i\right)-B &\ , \ & s_{k+2}=\left(\sum_{i=1}^k s_i\right)+B \end{array}\end{displaymath}

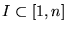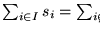Tenemos que ${\displaystyle \sum_{i=1}^n} s_i=4\left(\sum_{i=1}^k s_i\right)$. Por tanto, si $I\subset [1,n]$ es tal que $\sum_{i\in I}s_i=\sum_{i\not\in I}s_i$ entonces ambas sumas deben igualar el valor $2\left(\sum_{i=1}^k s_i\right)$. Entonces, los sumandos sk+1 y sk+2 deben estar en sumas distintas. Sus diferencias determinan pues un atercetamiento M' en M. Resumiendo: PARTITION es un problema completo-NP.
next up previous contents
Siguiente: Problemas en gráficas Un nivel arriba: Combinatoria Anterior: Atercetamientos (3DM):
Guillermo Morales-Luna
2000-07-10