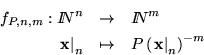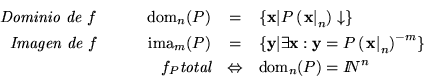Siguiente: Máquinas de Turing
Un nivel arriba: Conceptos básicos
Anterior: Reglas de transformación
Las funciones computables son las que se calculan por programas-while .
Si P es un programa-while y
![$[x_1\ldots x_k]$](img148.gif) es la lista de variables en P entonces consideraremos a las primeras variables como variables de entrada y a las últimas como de salida, de manera sólo un poco más precisa, para
es la lista de variables en P entonces consideraremos a las primeras variables como variables de entrada y a las últimas como de salida, de manera sólo un poco más precisa, para 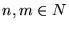 consideraremos
consideraremos
El programa P calcula, o computa, a la función
donde
En este caso definimos,
En adelante omitiremos los subíndices n,m y k.
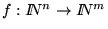 es computable si existe un programa-while tal que f=fP.
es computable si existe un programa-while tal que f=fP.
Guillermo Morales-Luna
2000-07-10
![\begin{eqnarray*}\mbox{\bf x}_n={[x_1\ldots x_n]} &:&\mbox{\rm lista de variable...
... x_{k-1}x_k]} &:&\mbox{\rm lista de variables de {\em salida}}
\end{eqnarray*}](img156.gif)
![\begin{eqnarray*}\mbox{\bf x}_n={[x_1\ldots x_n]} &:&\mbox{\rm lista de variable...
... x_{k-1}x_k]} &:&\mbox{\rm lista de variables de {\em salida}}
\end{eqnarray*}](img156.gif)