



Siguiente: Pruebas por contradicción
Un nivel arriba: COMPUTABILIDAD Y COMPLEJIDAD
Anterior: Contents
En matemáticas, la veracidad de una proposición queda asentada sólo cuando se la demuestra. Para aceptar una proposición cuantificada universalmente, es decir, de la forma ``Todo x cumple 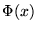 '', es insuficiente demostrar que para algunos posibles ``testigos''
'', es insuficiente demostrar que para algunos posibles ``testigos''
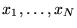 se ha probado que efectivamente se cumple
se ha probado que efectivamente se cumple 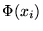 ,
con
,
con
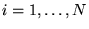 ,
por muy grande que sea N, pues aunque haya evidencia de que muchos puntos satisfacen al predicado
,
por muy grande que sea N, pues aunque haya evidencia de que muchos puntos satisfacen al predicado 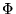 ,
ésta no basta para concluir que ``todos'' los puntos lo satisfacen.
Dos maneras típicas de demostrar proposiciones cuantificadas universalmente son los razonamientos por contradicción y, cuando el conjunto de puntos es numerable, por inducción. Las primeras dos secciones de este capítulo se abocan a la presentación de esos métodos de demostración.
Posteriormente presentamos los métodos de Cantor para mostrar como numerables a los productos finitos de conjuntos numerables. Esto es de particular importancia en la Teoría de la Complejidad pues permite construir una enumeración efectiva de los ``programas'' en un esquema de programación que sea efectivamente ``computable''.
Como una primera aproximación a la noción de ``computabilidad'' presentamos a los programas-while como un lenguaje formal de programación, con sintaxis y semántica bien definidos, y, finalmente, a través de ellos introducimos la noción de funciones computables.
Introducimos, luego, a las máquinas de Turing
,
ésta no basta para concluir que ``todos'' los puntos lo satisfacen.
Dos maneras típicas de demostrar proposiciones cuantificadas universalmente son los razonamientos por contradicción y, cuando el conjunto de puntos es numerable, por inducción. Las primeras dos secciones de este capítulo se abocan a la presentación de esos métodos de demostración.
Posteriormente presentamos los métodos de Cantor para mostrar como numerables a los productos finitos de conjuntos numerables. Esto es de particular importancia en la Teoría de la Complejidad pues permite construir una enumeración efectiva de los ``programas'' en un esquema de programación que sea efectivamente ``computable''.
Como una primera aproximación a la noción de ``computabilidad'' presentamos a los programas-while como un lenguaje formal de programación, con sintaxis y semántica bien definidos, y, finalmente, a través de ellos introducimos la noción de funciones computables.
Introducimos, luego, a las máquinas de Turing![[*]](../images/spanish/icons.gif/foot_motif.gif) . Tales máquinas aportan un enfoque alternativo al concepto de ``computabilidad'', sin embargo es equivalente al anterior. Probada esa equivalencia, terminaremos de presentar, de manera introductoria, a las funciones computables. Posteriormente, enunciamos la tesis de Church
. Tales máquinas aportan un enfoque alternativo al concepto de ``computabilidad'', sin embargo es equivalente al anterior. Probada esa equivalencia, terminaremos de presentar, de manera introductoria, a las funciones computables. Posteriormente, enunciamos la tesis de Church![[*]](../images/spanish/icons.gif/foot_motif.gif) .
A las funciones computables es posible presentarlas también como elementos de clases mínimas de funciones que contienen a un cierto conjunto de funciones y que son cerradas bajo algunos esquemas de composición. De tales enfoques nos ocuparemos en este primer capítulo.
Finalmente, veremos que la clase de programas formales, la de las máquinas de Turing y la de las funciones computables son todas numerables. Dado que la clase de todas las funciones
.
A las funciones computables es posible presentarlas también como elementos de clases mínimas de funciones que contienen a un cierto conjunto de funciones y que son cerradas bajo algunos esquemas de composición. De tales enfoques nos ocuparemos en este primer capítulo.
Finalmente, veremos que la clase de programas formales, la de las máquinas de Turing y la de las funciones computables son todas numerables. Dado que la clase de todas las funciones
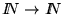 posee la misma cardinalidad de los números reales tenemos inmediatamente que hay muchas más funciones no-computables que computables.
posee la misma cardinalidad de los números reales tenemos inmediatamente que hay muchas más funciones no-computables que computables.




Siguiente: Pruebas por contradicción
Un nivel arriba: COMPUTABILIDAD Y COMPLEJIDAD
Anterior: Contents
Guillermo Morales-Luna
2000-07-10