Siguiente: Enteros algebraicos Un nivel arriba: Problemas en teoría de Anterior: .

DSP

Para cada 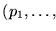$i\leq m$ consideremos los polinomios lineales

$$\begin{eqnarray*}f_i(\mbox{\bf X}) &=& \mbox{\bf a}_{i1}\cdot\mbox{\bf X}+a_{i,n... ...}\cdot\mbox{\bf X}+b_{i,n+1} =\sum_{j=1}^n b_{ij}X_j+b_{i,n+1} \end{eqnarray*}$$

El problema DSP coincide con el de decidir la validez de la fórmula

$$\begin{eqnarray*}\exists x_1\;\ldots\;\exists x_n&&\bigwedge_{i=1}^m [f_i(\mbox{... ...n&&\forall i\leq m: [f_i(\mbox{\bf x})\vert g_i(\mbox{\bf x})] \end{eqnarray*}$$

Para n=1 y $a_{i1}=0,b_{i1}=1\; \forall i\leq m$, el problema queda de la forma

$$\exists x\bigwedge_{i=1}^m [a_{i2}\vert x+b_{i2}] .$$

El Teorema Chino del Residuo estipula que el anterior problema tiene solución si y sólo si

$$\forall i_1,i_2\leq m:\; i_1\not=i_2\;\Rightarrow\; \mbox{\rm m.c.d.}(a_{i_12},a_{i_22})\vert(b_{i_12}-b_{i_22}).$$

DSP es pues una generalización del Teorema Chino del Residuo. Pero resulta ser completo-NP.